题目内容
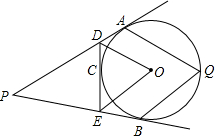 如图,从⊙O外一定点P作⊙O的两条切线,若C为
如图,从⊙O外一定点P作⊙O的两条切线,若C为 |
| AB |
 |
| AB |
(1)求证:△PDE的周长为定值,并求出定值;
(2)求证:∠DOE的度数为定值,并求出定值.
考点:切线的性质
专题:
分析:(1)首先证明DA=DC,EB=EC,进而证明PA=PB,即可解决问题;
(2)首先证明△ODA≌△ODC,进而得到∠AOD=∠COD,∠BOE=∠COE,即可解决问题.
(2)首先证明△ODA≌△ODC,进而得到∠AOD=∠COD,∠BOE=∠COE,即可解决问题.
解答: 证明:(1)如图,
证明:(1)如图,
∵DA、DC分别为⊙O的切线,
∴DA=DC;
同理可证:EB=EC,
∴DE=DA+EB;
∴PD+PE+DE=PA+PB;
∵PA、PB为⊙O的切线,
∴PA=PB=a,
∴△PDE的周长为定值,定值为2a.
(2)如图,连接OA、OB;
∵PA、PB分别为⊙0的切线,
∴OA⊥PA,OB⊥PB,
∴∠P+∠AOB=180°,
∴∠AOB=180°-∠P=180°-α;
∵DA、DC为⊙O的切线,
∴OA⊥DA,OB⊥EB;
在△ODA与△ODC中,
,
∴△ODA≌△ODC(HL),
∴∠AOD=∠COD,
同理可证:∠BOE=∠COE,
∴∠DOE=
∠AOB=90°-
α,
故∠DOE的度数为定值,定值为90°-
α.
 证明:(1)如图,
证明:(1)如图,∵DA、DC分别为⊙O的切线,
∴DA=DC;
同理可证:EB=EC,
∴DE=DA+EB;
∴PD+PE+DE=PA+PB;
∵PA、PB为⊙O的切线,
∴PA=PB=a,
∴△PDE的周长为定值,定值为2a.
(2)如图,连接OA、OB;
∵PA、PB分别为⊙0的切线,
∴OA⊥PA,OB⊥PB,
∴∠P+∠AOB=180°,
∴∠AOB=180°-∠P=180°-α;
∵DA、DC为⊙O的切线,
∴OA⊥DA,OB⊥EB;
在△ODA与△ODC中,
|
∴△ODA≌△ODC(HL),
∴∠AOD=∠COD,
同理可证:∠BOE=∠COE,
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
故∠DOE的度数为定值,定值为90°-
| 1 |
| 2 |
点评:该命题主要考查了切线的性质、切线长定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理后解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数y=-x+m的图象与x轴交于负半轴,则m的值可能为( )
| A、-2 | B、0 | C、2 | D、4 |
 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-1,0)三点,
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(-1,0)三点,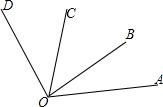 如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?
如图所示,∠AOB=35°,∠AOD=105°,∠COA=70°,试问在图中,哪条射线是哪个角的角平分线?