题目内容
4.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A,B,与x轴交于点E,F,且B,E两点的坐标分别为B(2,$\frac{3}{2}$),E(-1,0).(1)求二次函数的解析式;
(2)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴于点N,连接PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并求出S的最大值;
(3)在抛物线上是否存在点Q,使△QBF为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

分析 (1)根据矩形性质确定点A坐标,再把抛物线经过的三个点坐标代入求解即可;
(2)先求出直线BE,MN的解析式,再求出与抛物线对称轴的交点P,G,表示出线段PG的长度,根据三角形面积公式列出二次函数即可求最值;
(3)根据垂直设出直线解析式并求出解析式,联立抛物线即可求出点Q的坐标.
解答 解:(1)
由矩形性质可知,OA=BC=$\frac{3}{2}$,点A(0,$\frac{3}{2}$),
二次函数y=ax2+bx+c的图象经过A,B(2,$\frac{3}{2}$),E(-1,0),
∴$\left\{\begin{array}{l}{\frac{3}{2}=c}\\{\frac{3}{2}=4a+2b+c}\\{0=a-b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=\frac{3}{2}}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{2}{x}^{2}+x+\frac{3}{2}$;
(2)如图1
由抛物线的解析式为:y=-$\frac{1}{2}{x}^{2}+x+\frac{3}{2}$可求其对称轴为:x=1,
令MN与抛物线对称轴的交点为G,
设直线BE的解析式为:y=mx+n,
把点B,E坐标代入得:$\left\{\begin{array}{l}{\frac{3}{2}=2m+n}\\{0=-m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=\frac{1}{2}}\end{array}\right.$,
所以直线BE的解析式为:y=$\frac{1}{2}$x+$\frac{1}{2}$,
当x=1时,y=1,
∴点P(1,1),
∵MN∥BE,
可设直线MN的解析式为:y=$\frac{1}{2}$x+q,
把点M(2,t)代入,解得:q=t-1,
∴直线MN的解析式为:y=$\frac{1}{2}$x+t-1,
当y=0时,解得x=2-2t,
∴点N(2-2t,0),
当x=1时,y=t-$\frac{1}{2}$,
∴点G(1,t-$\frac{1}{2}$),
∴PG=1-(t-$\frac{1}{2}$)=-t+$\frac{3}{2}$,
∴S△PMN=$\frac{1}{2}$×PG×(xM-xN)=$\frac{1}{2}$×(-t+$\frac{3}{2}$)×[2-(2-2t)]=-${t}^{2}+\frac{3}{2}t$,
∴当x=$\frac{3}{4}$时,S△PMN有最大值为$\frac{9}{16}$;
(3)
当∠QBF=90°时,如图2
∵BQ⊥BF,直线BF解析式为y=-$\frac{3}{2}$x+$\frac{9}{2}$,
∴设BQ的解析式为:y=$\frac{2}{3}$x+f,
把点B(2,$\frac{3}{2}$)代入,解得,f=$\frac{1}{6}$,
∴直线BQ:y=$\frac{2}{3}$x+$\frac{1}{6}$,
联立$\left\{\begin{array}{l}{y=\frac{2}{3}x+\frac{1}{6}}\\{y=-\frac{1}{2}{x}^{2}+x+\frac{3}{2}}\end{array}\right.$,
解得:x=$-\frac{4}{3}$或x=2(舍去),
此时y=$-\frac{13}{18}$,
∴此时Q($-\frac{4}{3}$,$-\frac{13}{18}$),
当∠BFQ=90°时,如图3
因为FQ⊥BF,
所以设直线FQ的解析式为:y=$\frac{2}{3}$x+e,
把点F(3,0)代入,解得,e=-2,
∴直线FQ的解析式为:y=$\frac{2}{3}$x-2,
联立$\left\{\begin{array}{l}{y=\frac{2}{3}x-2}\\{y=-\frac{1}{2}x+x+\frac{3}{2}}\end{array}\right.$,
解得:x=$-\frac{7}{3}$,或x=3(舍去),
此时y=$-\frac{32}{9}$,
所以此时Q($-\frac{7}{3}$,$-\frac{32}{9}$),
当∠BQF=90°时,由图象可知,不存在.
综上所述,△QBF为直角三角形时,点Q的坐标为:($-\frac{4}{3}$,$-\frac{13}{18}$),($-\frac{7}{3}$,$-\frac{32}{9}$).
点评 此题主要考查二次函数的综合问题,会根据点求抛物线和直线的解析式,会运用变量表示三角形面积并解决最值问题,会根据直角分析点的坐标的存在性是解题的关键.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
 如图.在图中,
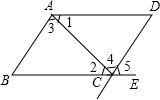
如图.在图中, 已知正方形ABCD中,以CD为边作等边三角形CED,连接BE与对角线AC交于点F,求证:EF=BF+CF.
已知正方形ABCD中,以CD为边作等边三角形CED,连接BE与对角线AC交于点F,求证:EF=BF+CF. 在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于20°.
在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于20°.