Question

14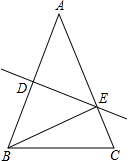．在△ABC中，AB=AC，DE垂直平分AB，∠EBC=30°，求∠A的度数．

Answer 1

分析 先线段垂直平分线的性质得到EA=EB，则利用等腰三角形的性质得∠A=∠EBA，设∠A=x，则∠EBA=x，∠ABC=x+30°，再由AB=AC得∠C=∠ABC=x+30°，然后根据三角形内角和定理得到x+x+30°+x+30°=180°，然后解方程求出x即可．

解答 解：∵DE垂直平分AB，
∴EA=EB，
∴∠A=∠EBA，
设∠A=x，则∠EBA=x，
∴∠ABC=∠EBA+∠EBC=x+30°，
∵AB=AC，
∴∠C=∠ABC=x+30°，
∵∠A+∠ABC+∠C=180°，
∴x+x+30°+x+30°=180°，解得x=40°，
即∠A的度数为40°．

点评 本题考查了线段垂直平分线的性质：线段的垂直平分线上任意一点，到线段两端点的距离相等．也考查了等腰三角形的性质．