题目内容
5.△ABC中,∠A=x,∠B、∠C的角平分线的夹角为y,则y与x之间的关系可以表示为y=90°+$\frac{1}{2}$x..分析 根据角平分线的性质得出∠1=∠2=$\frac{1}{2}$∠ABC,$∠3=∠4=\frac{1}{2}$∠ACB,根据三角形内角和定理得出y=180°-(∠1+∠3),∠ABC+∠ACB=180°-x,进而求得y=180°-$\frac{1}{2}$(180°-x)=90°+$\frac{1}{2}$x.
解答  解:∵PB、PC是∠B、∠C的角平分线,
解:∵PB、PC是∠B、∠C的角平分线,
∴∠1=∠2=$\frac{1}{2}$∠ABC,$∠3=∠4=\frac{1}{2}$∠ACB,
∴∠1+3=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB),
∵y=180°-(∠1+∠3),∠ABC+∠ACB=180°-x,
∴y=180°-$\frac{1}{2}$(180°-x)=90°+$\frac{1}{2}$x.
故答案为y=90°+$\frac{1}{2}$x.
点评 本题考查了角平分线的性质和三角形内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.若分式$\frac{x-1}{(x-2)(x-3)}$=$\frac{a}{x-3}$+$\frac{b}{x-2}$(a、b为常数),则a、b的值为( )
| A. | a=4,b=-3 | B. | a=2,b=-1 | C. | a=-1,b=1 | D. | a=-1,b=2 |
13.代数式4x2+1加上下列单项式后,仍不能成为完全平方式的是( )
| A. | 4x4 | B. | 4x | C. | -4x | D. | 2x |
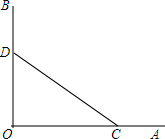 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.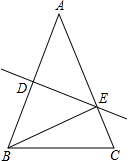 在△ABC中,AB=AC,DE垂直平分AB,∠EBC=30°,求∠A的度数.
在△ABC中,AB=AC,DE垂直平分AB,∠EBC=30°,求∠A的度数.