题目内容
13.关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根.(1)求m的取值范围;
(2)上述方程的根x1,x2恰好是斜边为6的直角三角形另外两边的边长,求这个三角形的周长.
分析 (1)由方程有两个实数根结合根的判别式,可得出△=8m-16≥0,解之即可得出结论;
(2)根据根与系数的关系可得出x1+x2=2(m+1)、x1•x2=m2+5,结合勾股定理可得出关于m的一元二次方程,解之可得出m的值,由方程的两根均为正值可确定m的值,再根据三角形的周长公式即可求出结论.
解答 解:(1)∵关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根,
∴△=[-2(m+1)]2-4(m2+5)=8m-16≥0,
解得:m≥2.
(2)∵x1,x2是方程x2-2(m+1)x+m2+5=0的两个根,
∴x1+x2=2(m+1),x1•x2=m2+5.
∵x12+x22=(x1+x2)2-2x1•x2=62,即m2+4m-21=0,
∴m=3或m=-7.
∵2(m+1)>0,
∴m=3,
∴这个三角形的周长=6+x1+x2=14.
点评 本题考查了根与系数的关系、根的判别式以及勾股定理,解题的关键是:(1)由方程有两个实数根找出△=8m-16≥0;(2)利用根与系数的关系结合勾股定理找出m2+4m-21=0.

练习册系列答案
相关题目
8.买x份报纸的总价为y元,根据下表,用含x的式子表示y,则x与y之间的关系是y=0.4x.
| 份数/份 | 1 | 2 | 3 | 4 | … |
| 价钱/元 | 0.4 | 0.8 | 1.2 | 1.6 | … |

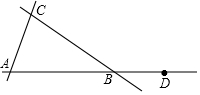 如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?
如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?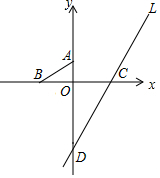 如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题: 如图,在直角三角形ABC中,∠ACB=90°,AC∥DE,CD∥EF,若∠ACD=45°,
如图,在直角三角形ABC中,∠ACB=90°,AC∥DE,CD∥EF,若∠ACD=45°,