题目内容
5. 如图,在直角三角形ABC中,∠ACB=90°,AC∥DE,CD∥EF,若∠ACD=45°,
如图,在直角三角形ABC中,∠ACB=90°,AC∥DE,CD∥EF,若∠ACD=45°,求证:EF平分∠DEB.
分析 根据平行线的性质得到∠DEB=∠ACB=90°,∠BEF=∠DCB=45°,证明结论.
解答 证明:∵∠ACB=90°,∠ACD=45°,
∴∠DCB=45°,
∵AC∥DE,
∴∠DEB=∠ACB=90°,
∵CD∥EF,
∴∠BEF=∠DCB=45°,
∴∠DEF=45°,
∴EF平分∠DEB.
点评 本题考查的是三角形内角和定理、平行线的性质,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
15.将下列多项式因式分解,结果中不含有因式a+1的是( )
| A. | a2-1 | B. | a2+a | C. | (a-1)2-a+1 | D. | (a+2)2-2(a+2)+1 |
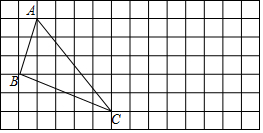 如图,网格中的小正方形都是边长为1个单位长度的小正方形.
如图,网格中的小正方形都是边长为1个单位长度的小正方形.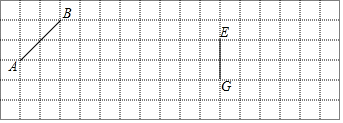
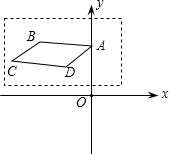 在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1).
在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1). 利用图中的网格线(最小的正方形的边长为1)画图;
利用图中的网格线(最小的正方形的边长为1)画图;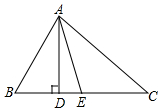 如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是34°.
如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是34°.