��Ŀ����
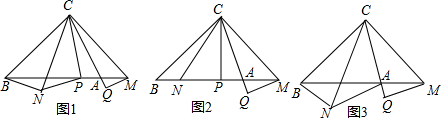
20���ڡ�ABC�У���ABC=45�㣬��BAC=75�㣬��M��BA�ӳ�����һ�㣬����CM��������CM��C��˳ʱ����ת60��õ�������CN������MCN��ƽ���߽�BA�ڵ�P������NP���ҡ�CPN=��CPM������BN������M��CA�Ĵ��ߣ�����Ϊ��Q����1����ͼ1����AC=4����BC�ij���
��2����ͼ2������N��AB����ʱ����֤��BN=$\sqrt{2}$MQ��
��3����ͼ3������N�ڡ�ACB�Ľ�ƽ������ʱ��ֱ��д��$\frac{M{Q}^{2}}{B{N}^{2}}$��ֵ��
���� ��1������A��AH��BC��H���������ֱ�������κͺ�30��ǵ�ֱ�������Σ�����AC�ij������CH��BH�ij������ɵõ�BC�ij���
��2������N��ND��BC��D�����ж���MCP�ա�NCP��ASA�����ó�CM=CN�����ж���MCQ�ա�NCD��AAS�����ó�QM=DN�������Rt��BDN�У����ݡ�B=45�㣬���BN=$\sqrt{2}$DN�����ɵõ�BN=$\sqrt{2}$MQ��
��3����N��ND��BC��D�����ݵ�N�ڡ�ACB�Ľ�ƽ�����ϣ��Լ���MCQ�ա�NCD���ɵ�AC��CP�غϣ����ж���BCM�ǵ���ֱ�������Σ��õ�BC=MC=NC�������ND=1����Rt��DCN�У����CN=2��CD=$\sqrt{3}$��QM=1�������õ�Rt��BDN�У�BN2=8-4$\sqrt{3}$���������$\frac{M{Q}^{2}}{B{N}^{2}}$��ֵ��
��� 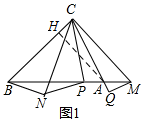 �⣺��1����ͼ1������A��AH��BC��H��
�⣺��1����ͼ1������A��AH��BC��H��
�ߡ�ABC=45�㣬��BAC=75�㣬
���ACB=60�㣬
���BAH=45�㣬��CAH=30�㣬
��AC=4��
��Rt��ACH��CH=$\frac{1}{2}$AC=2��AH=2$\sqrt{3}$��
��BH=2$\sqrt{3}$��
��BC=CH+BH=2+2$\sqrt{3}$��
��2��֤������ͼ2������N��ND��BC��D��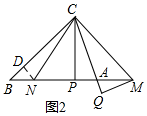
��CPƽ�֡�MCN��
���MCP=��NCP��
�ڡ�MCP�͡�NCP�У�
$\left\{\begin{array}{l}{��MCP=��NCP}\\{CP=CP}\\{��CPN=��CPM}\end{array}\right.$��
���MCP�ա�NCP��ASA����
��CM=CN��
�ߡ�BCA=��MCN=60�㣬
���MCQ=��NCD��
��MQ��CQ��ND��CD��
���Q=��CDN=90�㣬
�ڡ�MCQ�͡�NCD�У�
$\left\{\begin{array}{l}{��Q=��CDN}\\{��MCQ=��NCD}\\{CM=CN}\end{array}\right.$��
���MCQ�ա�NCD��AAS����
��QM=DN��
�֡�Rt��BDN�У���B=45�㣬
��BN=$\sqrt{2}$DN��
��BN=$\sqrt{2}$MQ��
��3����ͼ3����N��ND��BC��D��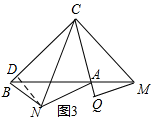
����N�ڡ�ACB�Ľ�ƽ������ʱ����BCN=��ACN=30�㣬
�ɣ�2���ɵã���MCQ�ա�NCD��
���BCN=��MCA��QM=DN��
���ACN=��ACM��
��ACƽ�֡�MAN��
�֡�CPƽ�֡�MAN��
��AC��CP�غϣ�
���MCA=��ACN=��BCN=30�㣬
���BCM=90�㣬
�ߡ�CBM=45�㣬
���BCM�ǵ���ֱ�������Σ�
�֡ߡ�MCP�ա�NCP��
��BC=MC=NC��
��ND=1����Rt��DCN��CN=2��CD=$\sqrt{3}$��QM=1��
��BC=2��BD=2-$\sqrt{3}$��
��Rt��BDN��BN2=BD2+DN2=��2-$\sqrt{3}$��2+12=8-4$\sqrt{3}$��
��$\frac{M{Q}^{2}}{B{N}^{2}}$=$\frac{{1}^{2}}{8-4\sqrt{3}}$=$\frac{2+\sqrt{3}}{4}$��
���� �������ڼ��α任�ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ�����ֱ�������ε��������ж��Լ����ɶ�����Ӧ�ã��������Ĺؼ����������߹���ȫ�������κ͵���ֱ�������Σ�����ȫ�������εĶ�Ӧ������Լ�����ֱ�������ε����ʽ��м�����⣮

| A�� | 2015 | B�� | 2016 | C�� | 2017 | D�� | 2018 |
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
 ��ͼ��һ��Բ���壬������Ϸ�������ͼ���ǣ�������
��ͼ��һ��Բ���壬������Ϸ�������ͼ���ǣ�������| A�� | ���������� | B�� | �ȱ������� | C�� | һ���� | D�� | Բ |
| A�� | 0.3��0.4��0.5 | B�� | 6��8��10 | C�� | 4��5��6 | D�� | $\frac{3}{5}$��$\frac{4}{5}$��1 |
| A�� | $\frac{a-2}{��a-2��^{2}}$ | B�� | $\frac{2a-4}{a-1}$ | C�� | $\frac{1}{a-2}$ | D�� | $\frac{a+2}{2a}$ |