题目内容
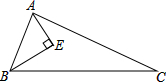 如图所示,在△ABC中,AE平分∠BAC,BE⊥AE,∠ABE=2∠C,求证:AC-AB=2BE.
如图所示,在△ABC中,AE平分∠BAC,BE⊥AE,∠ABE=2∠C,求证:AC-AB=2BE.考点:等腰三角形的判定与性质
专题:证明题
分析:延长BE交AC于M,根据三角形内角和可得∠3=∠4,可得AB=AM,再根据条件可证明MC=MB,可得到结论.
解答:证明:如图,延长BE交AC于M,
∵BE⊥AE,
∴∠AEB=∠AEM=90°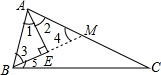 ,
,
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°-∠1,
同理,∠4=90°-∠2,
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM,
∵BE⊥AE,
∴BM=2BE,
∴AC-AB=AC-AM=CM,
∵∠4是△BCM的外角,
∴∠4=∠5+∠C,
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5,
∴3∠C=∠4+∠5=2∠5+∠C,
∴∠5=∠C,
∴CM=BM,
∴AC-AB=BM=2BE.
∵BE⊥AE,
∴∠AEB=∠AEM=90°
 ,
,在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°-∠1,
同理,∠4=90°-∠2,
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM,
∵BE⊥AE,
∴BM=2BE,
∴AC-AB=AC-AM=CM,
∵∠4是△BCM的外角,
∴∠4=∠5+∠C,
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5,
∴3∠C=∠4+∠5=2∠5+∠C,
∴∠5=∠C,
∴CM=BM,
∴AC-AB=BM=2BE.
点评:本题主要考查等腰三角形的判定和性质,构造等腰三角形,证得AC-AB=MC=BM是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长. 如图,在网格图中(小正方形的边长1),△ABC的三个顶点都在格点上.
如图,在网格图中(小正方形的边长1),△ABC的三个顶点都在格点上.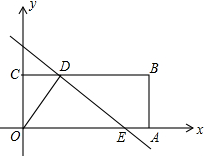 如图,四边形OABC是矩形,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
如图,四边形OABC是矩形,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-