题目内容
 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为
- A.
 a
a - B.
 a
a - C.(
 -1)a
-1)a - D.(2-
 )a
)a
B
分析:作出图象,把实际问题转化成数学问题,求出弦心距,再用半径减弦心距就可以了.
解答: 解:如图,正方形ABCD是圆内接正方形,BD=a,
解:如图,正方形ABCD是圆内接正方形,BD=a,
点O是圆心,也是正方形的对角线的交点,则OB= ,
,
△BOC是等腰直角三角形,
作OF⊥BC,垂足为F,由垂径定理知,点F是BC的中点,
∴OF=OBsin45°=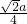 ,
,
∴x=EF=OE-OF= a.
a.
故选B.
点评:本题利用了正方形的性质,垂径定理,正弦的概念,等腰直角三角形的性质求解.
分析:作出图象,把实际问题转化成数学问题,求出弦心距,再用半径减弦心距就可以了.
解答:
 解:如图,正方形ABCD是圆内接正方形,BD=a,
解:如图,正方形ABCD是圆内接正方形,BD=a,点O是圆心,也是正方形的对角线的交点,则OB=
 ,
,△BOC是等腰直角三角形,
作OF⊥BC,垂足为F,由垂径定理知,点F是BC的中点,
∴OF=OBsin45°=
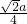 ,
,∴x=EF=OE-OF=
 a.
a.故选B.
点评:本题利用了正方形的性质,垂径定理,正弦的概念,等腰直角三角形的性质求解.

练习册系列答案
相关题目
 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )A、
| ||||
B、
| ||||
C、(
| ||||
D、(2-
|
 如图,用一块直径为1m的圆桌布平铺在对角线长为1m的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为1m的圆桌布平铺在对角线长为1m的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2-
|
 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为 为 ( ▲ )
为 ( ▲ )





 B.
B. C.
C. D.
D.