Question

5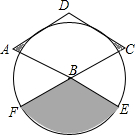．如图，菱形ABCD的边长为2，∠A=60°，以点B为圆心的圆与AD、DC相切，与AB、CB的延长线分别相交于点E、F，则图中阴影部分的面积为$\frac{π}{2}$+$\sqrt{3}$．

Answer 1

分析 设AD与圆的切点为G，连接BG，通过解直角三角形求得圆的半径，然后根据扇形的面积公式求得三个扇形的面积，进而就可求得阴影的面积．

解答 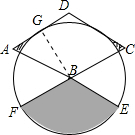解：设AD与圆的切点为G，连接BG，
∴BG⊥AD，
∵∠A=60°，BG⊥AD，
∴∠ABG=30°，
在直角△ABG中，BG=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$，AG=1，
∴圆B的半径为$\sqrt{3}$，
∴S_△ABG=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$
在菱形ABCD中，∠A=60°，则∠ABC=120°，
∴∠EBF=120°，
∴S_阴影=2（S_△ABG-S_扇形）+S_扇形FBE=2×（$\frac{\sqrt{3}}{2}$-$\frac{30π×3}{360}$）+$\frac{120π×3}{360}$=$\frac{π}{2}$+$\sqrt{3}$．
故答案为：$\frac{π}{2}$+$\sqrt{3}$．

点评 此题主要考查了菱形的性质以及切线的性质以及扇形面积等知识，正确利用菱形的性质和切线的性质求出圆的半径是解题关键．