题目内容
10.使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点.已知y=x2+kx-4(k为常数).(1)当k=0时,求该函数的零点;
(2)证明:无论k取何值,该函数总有两个零点.
分析 (1)根据函数的零点的定义,令y=0,解方程即可.
(2)令y=0,可得x2+kx-4=0.只要证明△=k2-4×(-4)=k2+16>0即可.
解答 解:(1)当k=0时,y=x2-4.
令y=0,x2-4=0,解得x=2或x=-2
∴当k=0时,该函数的零点是2和-2.
(2)证明:因为y=x2+kx-4,令y=0,可得x2+kx-4=0.
∵△=k2-4×(-4)=k2+16>0,
∴无论k取何值,方程x2+kx-4=0总有两个不相等的实数根,
∴无论k取何值,该函数总有两个零点.
点评 本题考查二次函数图象上点的特征、根的判别式、一元二次方程的解等知识,解题的关键是理解题意,用转化的思想思考问题.

练习册系列答案
相关题目
13.下列事件中,是必然事件的是( )
| A. | 打开电视机,它正在直播排球比赛 | |
| B. | 抛掷5枚硬币,结果是2个正面朝上与3个反面朝上 | |
| C. | 黑暗中从一大串钥匙中随便选中一把,用它打开了门 | |
| D. | 投掷一枚普通的正方体骰子,正面朝上的数不是奇数便是偶数 |
5.下列数据中最小的是( )
| A. | 11011001(二进制数) | B. | 75(十进制数) | ||
| C. | 72(八进制数) | D. | 57(十六制数) |
20.估计$\sqrt{16}$+$\sqrt{20}$的运算结果应在( )
| A. | 6与7之间 | B. | 7与8之间 | C. | 8与9之间 | D. | 9与10之间 |
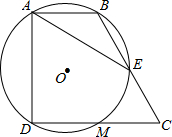 如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M. 如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$.
如图,在△ABC中CD⊥AB于点D,AC=8,BC=6,CD=$\sqrt{15}$. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?