题目内容
18.已知2014(x+3)2与$\frac{{\sqrt{x-y-4}}}{{{{2015}^2}}}$互为相反数,求$\sqrt{xy}$的整数部分的平方根.分析 根据相反数得出方程,根据偶次方和算术平方根的非负性得出x+3=0,x-y-4=0,求出x、y,求出xy,求出$\sqrt{xy}$的整数部分,最后根据平方根定义求出即可.
解答 解:根据题意得:2014(x+3)2+$\frac{{\sqrt{x-y-4}}}{{{{2015}^2}}}$=0,
x+3=0,x-y-4=0,
解得:x=-3,y=-7,
xy=21,
∵4<$\sqrt{21}$<5,
∴$\sqrt{xy}$的整数部分为4,
∴$\sqrt{xy}$的整数部分的平方根是±2.
点评 本题考查了算术平方根、平方根、估算无理数的大小、绝对值和算术平方根的非负性等知识点,能熟记每个知识点是解此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
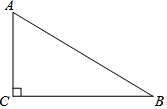 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.