题目内容
 如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为
如图,在△ABC中,AB=5,AC=4,△ABC绕着点A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之比为考点:旋转的性质
专题:
分析:根据旋转的性质,可得△ABC与△AB′C′的关系,根据两边对应成比例,夹角相等的三角形相似,可得△ABB′与△ACC′的关系,根据相似三角形面积的比等于相似比的平方,可得答案.
解答:解:△ABC绕着点A旋转后能与△AB′C′重合,
∴AB=AB′,AC=AC′,∠BAB′=∠CAC′,
∵
=
,∠BAB′=∠CAC′
∴△ABB′∽△ACC′,
∵
=
,
∴△ABB′与△ACC′的面积之比=(
) 2=
,
故答案为:
.
∴AB=AB′,AC=AC′,∠BAB′=∠CAC′,
∵
| AB |
| AC |
| AB′ |
| AC′ |
∴△ABB′∽△ACC′,
∵
| AB |
| AC |
| 5 |
| 4 |
∴△ABB′与△ACC′的面积之比=(
| 5 |
| 4 |
| 25 |
| 16 |
故答案为:
| 25 |
| 16 |
点评:本题考查了旋转的性质,先由旋转的性质得出三角形全等,再判定两个三角形相似,最后得出面积的比等于相似比的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
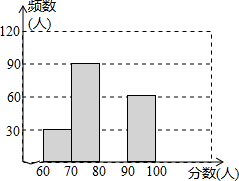 为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表.
为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表.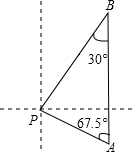 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1) 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为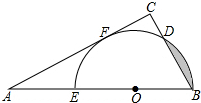 如图,把一块三角板(∠A=30°,∠C=90°,AC=6
如图,把一块三角板(∠A=30°,∠C=90°,AC=6 如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=
如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若OC:OA=1:2,且量得CD=12mm,则零件的厚度x=