题目内容
11. 如图,在正方形ABCD中,E是BC上的一点,BE=$\frac{1}{3}$BC,F是DC的中点,连接AE,EF.
如图,在正方形ABCD中,E是BC上的一点,BE=$\frac{1}{3}$BC,F是DC的中点,连接AE,EF.求证:∠AEF=∠DAE.
分析 延长EF交AD的延长线于G,由△DFG≌△CFE得DG=CE,FG=EF,设正方形边长为6k,则DG=CE=4k,DF=CF=3k,AD=6k,求出AG,EG,即可解决问题.
解答 证明:延长EF交AD的延长线于G,
∵四边形ABCD是正方形,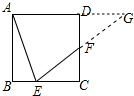
∴∠ADF=∠C=90°=∠FDG,
∵F是DC中点,
∴DF=FC,
在△DFG和△CFE中,
$\left\{\begin{array}{l}{∠FDG=∠C}\\{DF=CF}\\{∠DFG=∠CFE}\end{array}\right.$,
∴△DFG≌△CFE,
∴DG=CE,FG=EF,
设正方形边长为6k,则DG=CE=4k,DF=CF=3k,AD=6k,
在RT△DFG中,FG=$\sqrt{D{G}^{2}+D{F}^{2}}$=5k,
∴EF=FG=5k,
∴AG=AD+DG=10k,EG=EF+FG=10k,
∴∠AEF=∠DAE.
点评 本题考查全等三角形的判定和性质、正方形的性质、勾股定理等知识,解题的关键是添加辅助线构造全等三角形,学会设参数k,表示出相应的线段解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | a3+a3=a6 | B. | a3•a=a4 | C. | a6÷a2=a3 | D. | (2a2)3=6a5 |
3.下列方程中是一元二次方程的是( )
| A. | x+2y=1 | B. | 2x(x-1)=2x2+3 | C. | x2-2=0 | D. | 3x+$\frac{1}{x}$=4 |
1.若x>y,则下列变形正确的是( )
| A. | x+3>y+3 | B. | x-3<y-3 | C. | -3x>-3y | D. | -$\frac{x}{3}>-\frac{y}{3}$ |
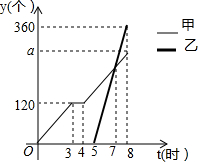 某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.
某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.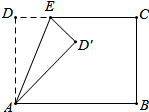 如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$.
如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$.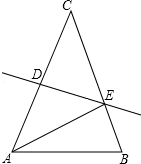 如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.
如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.