题目内容
 如图,在△ABC中,BE、CF是中线,且BE⊥CF,AC=b,AB=c(c>b)
如图,在△ABC中,BE、CF是中线,且BE⊥CF,AC=b,AB=c(c>b)(1)求BC的长;
(2)若△ABC存在,讨论
| b |
| c |
考点:三角形边角关系
专题:
分析:(1)O为△ABC重心,设OE=x,OF=y,则BO=2x,CO=2y,在Rt△COE、Rt△BOF、Rt△BOC中分别利用勾股定理,即可表示出BC的长.
(2)若△ABC存在,则c+b>BC和c-b<BC,由此得出不等式,解不等式,可得
的取值范围.
(2)若△ABC存在,则c+b>BC和c-b<BC,由此得出不等式,解不等式,可得
| b |
| c |
解答:解:(1)O为△ABC重心,设OE=x,OF=y,则BO=2x,CO=2y,
在Rt△COE、Rt△BOF、Rt△BOC中,有:
,
②-①得,3x2=BC2-
b2,
4×②-③,得:12x2=c2-BC2,
∴BC=
;
(2)若△ABC存在,则c+b>BC和c-b<BC,
得:
,
不等式④恒成立,不等式⑤2b2-5bc+2c2<0,
解得:
<
<2,
故当
<
<2时这样的三角形成立.
在Rt△COE、Rt△BOF、Rt△BOC中,有:
|
②-①得,3x2=BC2-
| 1 |
| 4 |
4×②-③,得:12x2=c2-BC2,
∴BC=
| 1 |
| 5 |
| 5(c2+b2) |
(2)若△ABC存在,则c+b>BC和c-b<BC,
得:
|
不等式④恒成立,不等式⑤2b2-5bc+2c2<0,
解得:
| 1 |
| 2 |
| b |
| c |
故当
| 1 |
| 2 |
| b |
| c |
点评:本题考查了三角形的三边关系,涉及了勾股定理、重心的性质及三角形的三边关系,解答本题需要同学们熟练掌握基础知识,掌握数形结合思想的运用.

练习册系列答案
相关题目
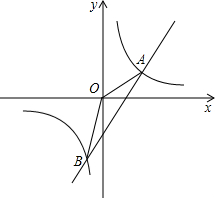 如图,一次函数y=ax-1(a≠0)的图象与反比例函数y=
如图,一次函数y=ax-1(a≠0)的图象与反比例函数y= 如表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
如表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题