题目内容
7.顺次连接平行四边形各边中点所形成的四边形是平行四边形.分析 可连接平行四边形的对角线,然后利用三角形中位线定理进行求解.
解答 解:如图;四边形ABCD是平行四边形,E、F、G、H分别是?ABCD四边的中点.
连接AC、BD;
∵E、F是AB、BC的中点,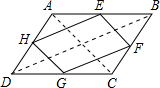
∴EF是△ABC的中位线;
∴EF∥AC;
同理可证:GH∥AC∥EF,EH∥BD∥FG;
∴四边形EFGH是平行四边形.
故顺次连接平行四边形各边中点的图形为平行四边形.
故答案为:平行四边形.
点评 此题考查了中点四边形,平行四边形的性质和判定,熟练掌握三角形中位线定理是解本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |
2.甲、乙两班学生人数相同,在同一次数学单元测试中,班级平均分和方差如下:$\overline{x}$甲=$\overline{x}$乙=80,s甲2=240,s乙2=180,则成绩较为稳定的班级是( )
| A. | 甲班 | B. | 乙班 | ||
| C. | 两班成绩一样稳定 | D. | 无法确定 |
12.下表是某班学生右眼视力的检查结果
(1)求该班学生右眼视力的平均值;
(2)求该班学生右眼视力的众数和中位数.
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 4 | 5 | 3 | 5 | 1 | 1 | 5 | 9 | 5 |
(2)求该班学生右眼视力的众数和中位数.
19.下列计算中,正确的是( )
| A. | (a+b)2=a2+b2 | B. | (2a-b)2=4a2-b2 | C. | (x+3)(x-2)=x2-6 | D. | (x+3)(x-3)=x2-9 |
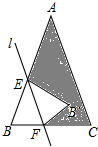 等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断:
等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断: