题目内容
1.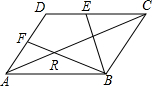 如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.
如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.
分析 由四边形ABCD是平行四边形,可得AD∥BC,AD=BC,即可证得△ARF∽△CRB,然后由F是DA的中点,根据相似三角形的对应边成比例,即可证得结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ARF∽△CRB,
∴AF:BC=FR:BR,
∵F是DA的中点,
∴AF=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴FR:BR=1:2,
∴FR=$\frac{1}{3}$BF,
即R为BF的三等分点.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意相似三角形的对应边成比例.

练习册系列答案
相关题目
9.已知点P(-3,4),则点P到x轴的距离和到y轴的距离分别为( )
| A. | 3,4 | B. | -3,4 | C. | 4,3 | D. | 4,-3 |
 如图,?ABCD中,∠B+∠D=144°,则∠D=72°.
如图,?ABCD中,∠B+∠D=144°,则∠D=72°.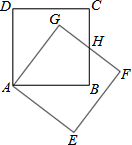 如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.
如图,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.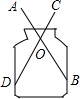 如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由. 数学应用:
数学应用: