题目内容
11.求函数的最大值 $\left\{\begin{array}{l}{S=-{t}^{2}+6t}&{(0<t≤2)}\\{S=-\frac{3}{4}{t}^{2}+4t+3}&{(2<t≤3)}\end{array}\right.$.分析 求出当0<t≤2时,函数取得最大值为8;再求出当2<t≤3时,函数取得最大值为$\frac{25}{3}$;从而求出函数的最大值为$\frac{25}{3}$.
解答 解:当0<t≤2时,S=-(t2-6t)=-(t2-6t+32-32)=-(t2-6t+32)+9=-(t-3)2+9,当t=2时,函数取得最大值为8;
当2<t≤3时,S=-$\frac{3}{4}$(t2-$\frac{16}{3}$t)+3=-$\frac{3}{4}$[t2-$\frac{16}{3}$t+($\frac{8}{3}$)2-($\frac{8}{3}$)2]+3=-$\frac{3}{4}$(t-$\frac{8}{3}$)2+$\frac{16}{3}$+3=-$\frac{3}{4}$(t-$\frac{8}{3}$)2+$\frac{25}{3}$,当t=$\frac{8}{3}$时,函数取得最大值为$\frac{25}{3}$.
故函数最大值为$\frac{25}{3}$.
点评 本题考查了二次函数的最值,利用配方法分别求出二次函数最值,再求出其中最大者即为函数最大值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在下列四个一元二次方程中,没有实数根的一个是( )
| A. | x2-8x+1=0 | B. | 2x2+1=3x | C. | 3x2-6x+4=0 | D. | (x-2)2-1=0 |
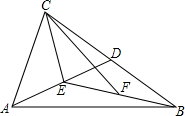 如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.
如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.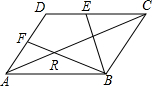 如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.
如图,在?ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,E,F分别为DC,DA的中点,求证:R为BF的三等分点.