题目内容
4. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)求证:△AEF≌△DEC;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
分析 (1)根据两直线平行,内错角相等求出∠AFE=∠DCE,∠FAE=∠CDE,然后利用“角角边”证明△AEF和△DEC全等;
(2)由(1)知AF平行等于BD,易证四边形AFBD是平行四边形,而AB=AC,AD是中线,利用等腰三角形三线合一定理,可证AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
解答 (1)证明:∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
$\left\{\begin{array}{l}{∠AFE=∠DCE}\\{∠EAF=∠CDE}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEC(AAS);
(2)解:若AB=AC,则四边形AFBD是矩形.理由如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.
点评 本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.端午节前夕,某超市用1680元购进A、B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=60}\\{36x+24y=1680}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=60}\\{24x+36y=1680}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{36x+24y=60}\\{x+y=1680}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{24x+36y=60}\\{x+y=1680}\end{array}\right.$ |
16.某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.

(1)收回的问卷份数为200,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
| 编号 | 教学方式 | 最喜欢的频数 | 频率 |
| 1 | 教师讲,学生听 | 20 | 0.10 |
| 2 | 教师提出问题,学生探索思考 | ||
| 3 | 学生自行阅读教材,独立思考 | 30 | |
| 4 | 分组讨论,解决问题 | 0.25 |

(1)收回的问卷份数为200,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
13.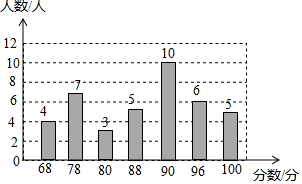 2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.
2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.
(1)结合以上信息完成下表:
(2)根据评价标准,96分以上(含96分)可评为优秀,该校八年级共有学生500名若全部参加测试,估计有多少学生的成绩能达到优秀?
(3)张明同学的数学成绩为88分,他认为自己成绩超过平均分,排名应该处于中上等水平,这种说法对吗?为什么?
 2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.
2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.(1)结合以上信息完成下表:
| 平均成绩(分) | 中位数(分) | 众数(分) |
| 86.85 | 90 | 90 |
(3)张明同学的数学成绩为88分,他认为自己成绩超过平均分,排名应该处于中上等水平,这种说法对吗?为什么?

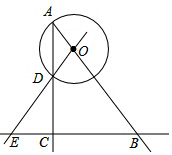 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.
 如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF.
如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF.