题目内容
20.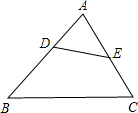 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.(1)求证:AD•AB=AE•AC;
(2)如果△ABC的面积为m,DE=3,BC=5,求△ADE的面积.
分析 (1)先根据相似三角形的判定定理可求出△AED∽△ABC,再由相似三角形的对应边成比例即可解答;
(2)根据相似三角形的性质即可得到结论.
解答 (1)证明:∵∠A=∠A,∠ADE=∠C,
∴△AED∽△ABC,
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
∴AD•AB=AE•AC;
(2)解:由(2)证得△AED∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ACB}}$=$\frac{DE}{BC}$,
∵△ABC的面积为m,DE=3,BC=5,
∴S△ADE=($\frac{DE}{BC}$)2•S△ABC=$\frac{9}{25}$m.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
11. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠3 | D. | ∠3+∠4=180° |
15.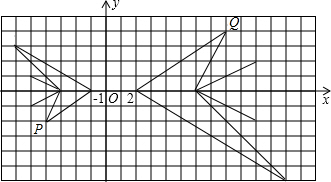 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )| A. | (-2a,-2b) | B. | (-a,-2b) | C. | (-2b,-2a) | D. | (-2a,-b) |
9.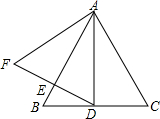 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )| A. | 30° | B. | 35° | C. | 55° | D. | 60° |
10.-(-3)的相反数的倒数是( )
| A. | -$\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | -3 |
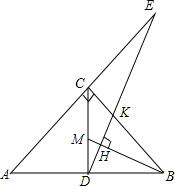 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证: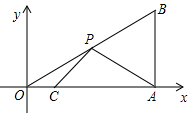 如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.
如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.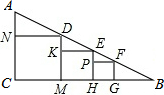 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8. 如图,将一副三角板的直角顶点重合,若∠CAD=130°,则两三角板重合部分形成的角∠BAE=50°.
如图,将一副三角板的直角顶点重合,若∠CAD=130°,则两三角板重合部分形成的角∠BAE=50°.