题目内容
5.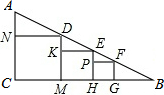 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.(1)求正方形HPFG的边长;
(2)写出第四个正方形的边长,从第三个正方形起,第p个正方形的边长是多少?直接写出结果.
分析 (1)由条件可证明△DKE∽△EPF,再结合正方形的性质,可分别表示出DK、PE,代入可求得PF,可得到答案;
(2)由已知条件DN=10=10×($\frac{4}{5}$)0,KE=8=10×($\frac{4}{5}$)1,PF=$\frac{32}{5}$=10×($\frac{4}{5}$)2,找到规律第n个正方形的边长=10×($\frac{4}{5}$)n-1,从而求解.
解答 解:∵四边形NCMD、四边形KMHE均为正方形,
∴∠DKE=∠DKE,KE∥PF,
∴∠DEK=∠EFP,
∴△DKE∽△EPF,
∴$\frac{DK}{PE}$=$\frac{KE}{PF}$,
又∵DK=10-8=2,KE=8,PE=8-PF,
∴$\frac{2}{8-PF}$=$\frac{8}{PF}$,
解得PF=$\frac{32}{5}$,
即正方形HGFP的边长为$\frac{32}{5}$;
(2)∵DN=10=10×($\frac{4}{5}$)0,
KE=8=10×($\frac{4}{5}$)1,
PF=$\frac{32}{5}$=10×($\frac{4}{5}$)2,
∴第四个正方形的边长=10×($\frac{4}{5}$)3=$\frac{128}{25}$,
∴第n个正方形的边长=10×($\frac{4}{5}$)n-1,
∴从第三个正方形起,第p个正方形的边长=10×($\frac{4}{5}$)p+2.
点评 本题考查了正方形的性质,相似三角形的判定与性质,解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系.

练习册系列答案
相关题目
13. 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )| A. | L≤40.2 | B. | L≥39.98 | C. | 39.98≤L≤40.02 | D. | 39.8≤L≤40.2 |
17.若关于x的分式方程$\frac{x-m}{x-1}-\frac{3}{x}$=1无解,则m的值为( )
| A. | 0 | B. | 1 | C. | -2 | D. | 1或-2 |
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2015的坐标为( )
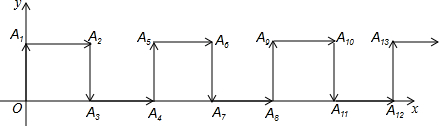

| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
15.等腰三角形的腰上的高线与底边的夹角为45°,若底边上的高为5,则此等腰三角形的面积为( )
| A. | 5 | B. | 10 | C. | 20 | D. | 25 |
 如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.
如图:矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,试判断四边形CODP的形状.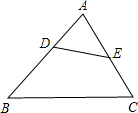 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.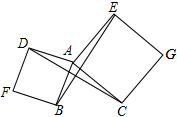 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.