题目内容
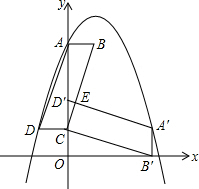 如图,在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),将?ABCD绕点C沿顺时针方向旋转90°,得到?A′B′CD′,A′D′与BC相交于点E.
如图,在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),将?ABCD绕点C沿顺时针方向旋转90°,得到?A′B′CD′,A′D′与BC相交于点E.(1)求经过点D、A、A′的抛物线的函数关系式;
(2)求?ABCD与?A′B′CD′的重叠部分(即△CED’)的面积;
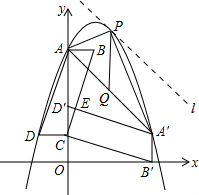
(3)点P是抛物线上点A、A′之间的一动点,是否存在点P使得△APA′的面积最大?若存在,求出△APA′的最大面积,及此时点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)设抛物线的解析式为y=ax2+bx+c,根据平行四边形的性质和旋转的性质易求点D的坐标和A′坐标,再把D(-1,1)、A(0,4)、A′(3,1)代入求出a、b、
c的值即可;
(2)根据旋转:∠CED’=90°,所以可证明△CED′∽△CAB,利用相似三角形的性质:面积比等于相似比的平方即可求出?ABCD与?A′B′CD′的重叠部分(即△CED’)的面积;
(3)易得:yAA'=-x+4,设P(t,-t2+2t+4),则Q(t,-t+4),所以PQ=(-t2+2t+4)-(-t+4)=-t2+3t,利用三角形的面积公式即可得到s和t的二次函数关系式利用函数的性质即可求出△APA′的最大面积,进而可求出点P的坐标.
c的值即可;
(2)根据旋转:∠CED’=90°,所以可证明△CED′∽△CAB,利用相似三角形的性质:面积比等于相似比的平方即可求出?ABCD与?A′B′CD′的重叠部分(即△CED’)的面积;
(3)易得:yAA'=-x+4,设P(t,-t2+2t+4),则Q(t,-t+4),所以PQ=(-t2+2t+4)-(-t+4)=-t2+3t,利用三角形的面积公式即可得到s和t的二次函数关系式利用函数的性质即可求出△APA′的最大面积,进而可求出点P的坐标.
解答:解:(1)∵四边形ABCD是平行四边形,将?ABCD绕点C沿顺时针方向旋转90°,得到?A′B′CD′,
顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),
∴D(-1,1)、A′(3,1),
设抛物线的解析式为y=ax2+bx+c,
将D(-1,1)、A(0,4)、A′(3,1)代入得:
,
解得:
,
∴y=-x2+2x+4或:y=-(x-1)2+5;
(2)根据旋转:∠CED’=90°,
∴△CED′∽△CAB,
∴
=(
)2,
即
=(
)2,
∴S△CED′=
;
或易得:yBC=3x+1与yA′D′=-
x+2,
由
得:E(
,
),
∴S△CED′=
=
;
(3)易得:yAA'=-x+4
设P(t,-t2+2t+4),则Q(t,-t+4),
∴PQ=(-t2+2t+4)-(-t+4)=-t2+3t,
∴S△APA′=
=-
(t-
)2+
,
∴△APA’的最大面积为
,
此时,P(
,
).
顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),
∴D(-1,1)、A′(3,1),
设抛物线的解析式为y=ax2+bx+c,
将D(-1,1)、A(0,4)、A′(3,1)代入得:
|
解得:
|

∴y=-x2+2x+4或:y=-(x-1)2+5;
(2)根据旋转:∠CED’=90°,
∴△CED′∽△CAB,
∴
| S△CED′ |
| S△CAB |
| CD′ |
| CB |
即
| S△CED′ | ||
|
| 1 | ||
|
∴S△CED′=
| 3 |
| 20 |
或易得:yBC=3x+1与yA′D′=-
| 1 |
| 3 |
由
|
| 3 |
| 10 |
| 19 |
| 10 |
∴S△CED′=
1×
| ||
| 2 |
| 3 |
| 20 |
(3)易得:yAA'=-x+4
设P(t,-t2+2t+4),则Q(t,-t+4),
∴PQ=(-t2+2t+4)-(-t+4)=-t2+3t,
∴S△APA′=
| (-t2+3t)•3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴△APA’的最大面积为
| 27 |
| 8 |
此时,P(
| 3 |
| 2 |
| 19 |
| 4 |
点评:本题着重考查了待定系数法求二次函数解析式以及二次函数的性质、平行四边形的性质、相似三角形的判定和性质、函数图象的交点等知识点,综合性强,同时也考查了数形结合的数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
四个实数-2,0,-
,1中,最大的实数是( )
| 2 |
| A、-2 | ||
| B、0 | ||
C、-
| ||
| D、1 |
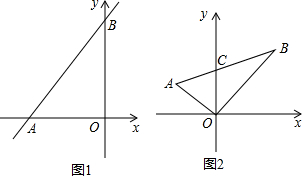 如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且
如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且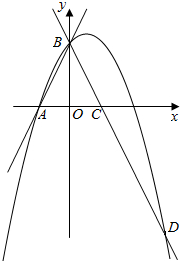 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).