题目内容
过矩形ABCD的顶点D，作DE⊥AC，垂足为E，若AE=8cm，ED=2cm，则矩形的周长是 ．
考点：矩形的性质
专题：
分析：根据勾股定理求AC，根据相似三角形的判定推出△DAE∽△CDA，求出AC，根据勾股定理求出DC，即可求出答案．
解答：
解：如图：
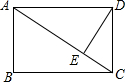
∵DE⊥AC，
∴∠DEA=90°，
∵AE=8cm，ED=2cm，
∴由勾股定理得：AD=
=
=2
（cm），
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，∠ADC=90°，
∵DE⊥AC，
∴∠AED=∠DEC=90°，
∵∠DAE=∠DAE，∠AED=∠ADC，
∴△DAE∽△CDA，
∴
=
，
∴
=
，
∴AC=
（cm），
在Rt△ADC中，由勾股定理得：DC=
=
=
（cm）
∴矩形ABCD的周长为2
+2×
=2
+
=5
（cm）．
故答案为：5
cm．
∵DE⊥AC，
∴∠DEA=90°，
∵AE=8cm，ED=2cm，
∴由勾股定理得：AD=
| 82+22 |
| 68 |
| 17 |
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，∠ADC=90°，
∵DE⊥AC，
∴∠AED=∠DEC=90°，
∵∠DAE=∠DAE，∠AED=∠ADC，
∴△DAE∽△CDA，
∴
| AD |
| AE |
| AC |
| AD |
∴
| ||
| 8 |
| AC | ||
|
∴AC=
| 17 |
| 2 |
在Rt△ADC中，由勾股定理得：DC=
| AC2-AD2 |
(
|
| ||
| 2 |
∴矩形ABCD的周长为2
| 68 |
| ||
| 2 |
| 68 |
| 17 |
| 17 |
故答案为：5
| 17 |
点评：本题考查了矩形的性质，勾股定理，相似三角形的性质和判定的应用，能综合运行性质进行推理和计算是解此题的关键，有一定的难度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，点D、E分别在边AB、AC上，下列比例式不能判定DE∥BC的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
0.0045用科学记数法表示为（ ）
| A、4.5×103 |
| B、4.5×10-3 |
| C、4.5×10-4 |
| D、0.45×10-5 |
已知：如图，在△ABC中，BC∥x轴，点A的坐标是（-4，3），点B的坐标是（-3，1）
如图，已知O是坐标原点，A、B、C三点的坐标分别为（1，0），（3，1），（2，3）．
如图，△ABC内接于⊙O，OD⊥BC于点D，∠A=55°，则∠OCD的度数是
如图，数轴上A、C两点对应的实数分别是1和2| 3 |
A、
| ||
B、1+
| ||
C、
| ||
D、2
|
如图，点D、F分别是等边△ABC的边CB、BA的延长线上一点，且BD=AF，连结CF，连结DA且延长交CF于点E．