题目内容
在△ABC中,∠C=30°,∠ABC=90°,点D、E分别为边AB、AC上的点,BD=CE,点F为AC中点,连接DF,点G为FD中点,连接AG,BE.

(1)求证:2AG=BE;
(2)延长AG交BE于M,过F作FN∥BE交AM于N,若GN=1,EM=2,求BM的长度.

(1)求证:2AG=BE;
(2)延长AG交BE于M,过F作FN∥BE交AM于N,若GN=1,EM=2,求BM的长度.
考点:全等三角形的判定与性质,等边三角形的判定与性质,含30度角的直角三角形
专题:计算题
分析:(1)首先可判断四边形ADHF是平行四边形,再由直角三角形30°角所对的边等于斜边一半可得,再根据全等三角形的判定和性质解答即可;
(2)根据全等三角形的判定和性质可得△EFM≌△HFN,利用全等三角形的性质解答即可.
(2)根据全等三角形的判定和性质可得△EFM≌△HFN,利用全等三角形的性质解答即可.
解答:
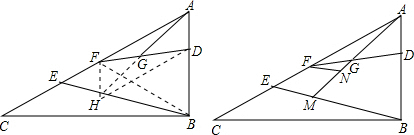 (1)证明:延长AG至H,使GH=AG,连接DH,FH,
(1)证明:延长AG至H,使GH=AG,连接DH,FH,
∵GD=GF,
四边形ADHF是平行四边形,
∴FH=AD,AF=DH.
连接BF,
∵在Rt△ABC中,∠ABC=90°,∠C=30°,AF=CF,
∴BF=AF=CF=AB,∠BAF=∠ABF=∠AFB=60°,
∵BD=CE,
∴AD=EF=FH,
∴∠HDA=∠BFE=120°,
∵DH=AF,
∴DH=BF,
在△ADH和△BFE中,
,
∴△ADH≌△BFE(SAS),
∴AH=BE=2AG;
(2)解:由(1)可知∠EFH=∠BAC=60°,∠AFH=60°=∠AFB,∠HAD=∠AHF=∠BEF,
∵FN∥BE,∠AFN=∠AEM,
∵∠HAD+∠HAE=∠BAC=∠AEB+∠HAE=∠AFN+∠HAE=60°,
∵∠EBF=∠AHD=∠HAF,
∴A、B、M、F四点共圆,∠AMF=∠ABF=60°,△FMN是等边△,
∴∠EFH+∠MFH=∠MFN+∠MFH,∠EFM=∠HFN,
∴△EFM≌△HFN(AAS),
∴ME=NH=2,
∴AH=BE=2AG=2GH=2(GN+ME)=2(1+2)=6,
∴BM=BE-EM=6-2=4.
 (1)证明:延长AG至H,使GH=AG,连接DH,FH,
(1)证明:延长AG至H,使GH=AG,连接DH,FH,∵GD=GF,
四边形ADHF是平行四边形,
∴FH=AD,AF=DH.
连接BF,
∵在Rt△ABC中,∠ABC=90°,∠C=30°,AF=CF,
∴BF=AF=CF=AB,∠BAF=∠ABF=∠AFB=60°,
∵BD=CE,
∴AD=EF=FH,
∴∠HDA=∠BFE=120°,
∵DH=AF,
∴DH=BF,
在△ADH和△BFE中,
|
∴△ADH≌△BFE(SAS),
∴AH=BE=2AG;
(2)解:由(1)可知∠EFH=∠BAC=60°,∠AFH=60°=∠AFB,∠HAD=∠AHF=∠BEF,
∵FN∥BE,∠AFN=∠AEM,
∵∠HAD+∠HAE=∠BAC=∠AEB+∠HAE=∠AFN+∠HAE=60°,
∵∠EBF=∠AHD=∠HAF,
∴A、B、M、F四点共圆,∠AMF=∠ABF=60°,△FMN是等边△,
∴∠EFH+∠MFH=∠MFN+∠MFH,∠EFM=∠HFN,
∴△EFM≌△HFN(AAS),
∴ME=NH=2,
∴AH=BE=2AG=2GH=2(GN+ME)=2(1+2)=6,
∴BM=BE-EM=6-2=4.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式的值一定是正数的是( )
| A、3a |
| B、a2+0.1 |
| C、(a+1)2 |
| D、a3+10 |
郑州地铁2号线是一条南北线,起于惠济区,一直到达南三环外的向阳路,2014年12月,郑州地铁2号线一期工程将通车试运营,据初步核算,一期工程估算投资总额为100.029亿元,数据100.029亿用科学记数法表示为( )
| A、10.0029×1010 |
| B、1.00029×1010 |
| C、1.00029×109 |
| D、0.100029×1011 |
 如图,已知线段BC平行于x轴,AB⊥x轴于点A,过点C的双曲线y=
如图,已知线段BC平行于x轴,AB⊥x轴于点A,过点C的双曲线y=
 已知△ABC三个顶点的坐标为A(-3,1),B(1,2),C(0,4),请在平面直角坐标系中画出△ABC关于x轴对称的图形△A′B′C′.
已知△ABC三个顶点的坐标为A(-3,1),B(1,2),C(0,4),请在平面直角坐标系中画出△ABC关于x轴对称的图形△A′B′C′.