题目内容
6.某农户在一荒坡上种植杨树和松树,已知种植的杨树棵数比松树棵数的一半多9棵.(1)若要求种植的松树棵数比总数的三分之一多3棵,则两种树各种了多少棵?
(2)若要求种植的松树棵数比总数的三分之一少,则至多要种植多少棵杨树?
分析 (1)可设种植杨树x棵,种植松树y棵,根据等量关系:①种植的杨树棵数比松树棵数的一半多9棵;②种植的松树棵数比总数的三分之一多3棵;列出方程组求解即可;
(2)可设种植杨树z棵,根据不等关系:要求种植的松树棵数比总数的三分之一少,列出不等式求解即可.
解答 解:(1)设种植杨树x棵,种植松树y棵,依题意有
$\left\{\begin{array}{l}{x=\frac{1}{2}y+9}\\{x=\frac{1}{3}(x+\frac{1}{2}y+9)+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=9}\\{y=0}\end{array}\right.$.
答:种植杨树9棵,种植松树0棵;
(2)设种植杨树z棵,则种植松树(2z-18)棵,依题意有
z<$\frac{1}{3}$(z+2z-18),
0<-6,
故不等式无解.
点评 本题考查二元一次方程组的应用和一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题意列出等量关系和不等关系式即可求解.

练习册系列答案
相关题目
11.下列命题中是真命题的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 对角线互相垂直且相等的四边形是正方形 | |
| C. | 两个等腰直角三角形一定相似 | |
| D. | 打开数学课本,恰好翻到第88页是必然事件 |
16.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
| A. | 27 | B. | 35 | C. | 44 | D. | 54 |
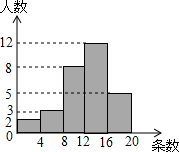 某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是A′(5,2).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是A′(5,2). 如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).