题目内容
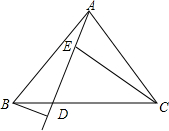
 如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,BD的垂直平分线MN交AB于的E,连接DE,求证:AB=AC+CD.
如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,BD的垂直平分线MN交AB于的E,连接DE,求证:AB=AC+CD.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:易证△ACD≌△AED,则有AC=AE,CD=ED,根据垂直平分线的性质可得ED=EB,即可证到AB=AE+EB=AC+CD.
解答:
解:∵MN是DB的垂直平分线,
∴ED=EB,
∴∠EDN=∠B ,
,
∴∠AED=∠EDN+∠B=2∠B
∵∠C=2∠B,
∴∠AED=∠C.
又∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD.
在△ACD和△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED,
∴AB=AE+BE=AC+ED=AC+CD.
∴ED=EB,
∴∠EDN=∠B
 ,
,∴∠AED=∠EDN+∠B=2∠B
∵∠C=2∠B,
∴∠AED=∠C.
又∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD.
在△ACD和△AED中,
|
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED,
∴AB=AE+BE=AC+ED=AC+CD.
点评:本题主要考查了全等三角形的判定与性质、垂直平分线的性质、等腰三角形的性质、三角形外角性质、角平分线的定义等知识,证到△ACD≌△AED是解决本题的关键.

练习册系列答案
相关题目
已知圆锥的母线为6,底面圆的半径为4,则此圆锥的侧面积是( )
| A、12π | B、15π |
| C、24π | D、30π |
 如图所示,△ABC中,AB=AC,∠BAC=80°,过点A作射线AD,点E在AD上,∠ADB=100°.∠CED=80°,
如图所示,△ABC中,AB=AC,∠BAC=80°,过点A作射线AD,点E在AD上,∠ADB=100°.∠CED=80°,