题目内容
16.已知函数y=(m2+2m)${x}^{{m}^{2}-m-1}$(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
分析 (1)根据y=kx(k是不等于零的常数)是正比例函数,可得答案;
(2)根据$y=\frac{k}{x}$(k≠0)转化为y=kx-1(k≠0)的形式.
解答 解:(1)由y=(m2+2m)${x}^{{m}^{2}-m-1}$是正比例函数,得
m2-m-1=1且m2+2m≠0,
解得m=2或m=-1;
(2)由y=(m2+2m)${x}^{{m}^{2}-m-1}$是反比例函数,得
m2-m-1=-1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x-1.
点评 本题考查了反比例函数的定义,重点是将一般式$y=\frac{k}{x}$(k≠0)转化为y=kx-1(k≠0)的形式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.一个圆柱体的半径比原来圆柱体的半径多3倍,高是原来的$\frac{1}{4}$,这个圆柱体体积是原来圆柱体体积的( )
| A. | $\frac{3}{4}$倍 | B. | 1倍 | C. | 2倍 | D. | 4倍 |
11.下列方程中,是一元一次方程的是( )
| A. | 3x-2y+z=0 | B. | $\frac{x}{7}$=-1 | C. | $\frac{2}{1-x}$=3 | D. | x2-x=1 |
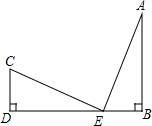 如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE.
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE.