题目内容
2.解答题(1)化简:2$\sqrt{2}$-3$\sqrt{2}$
(2)化简:$\sqrt{1+\frac{16}{9}}$
(3)解方程:$\frac{2y-1}{3}$+1=$\frac{y+2}{4}$.
分析 (1)原式合并同类二次根式即可得到结果;
(2)原式被开方数变形后,再利用算术平方根定义计算即可得到结果;
(3)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.
解答 解:(1)原式=-$\sqrt{2}$;
(2)原式=$\sqrt{\frac{25}{9}}$=$\frac{5}{3}$;
(3)去分母得:4(2y-1)+12=3(y+2),
去括号得:8y-4+12=3y+6,
移项合并得:5y=-2,
解得:y=-$\frac{2}{5}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.下列方程中,两个实数根之和等于2的是( )
| A. | x2-2x+3=0 | B. | x2+2x-3=0 | C. | 2x2-4x-1=0 | D. | x2-x-2=0 |
17.已知点P(a,b),ab>0,a+b>0,则点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
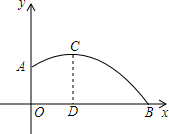 如图所示,一男生推铅球,铅球在点A处出手,出手时铅球离地面$\frac{5}{3}$m.铅球落地点在B处,铅球运行中在该男生前4m处(即0D=4)达到最高点,此时铅球离地面3m.根据图示的直角坐标系,你能算出该男生推铅球的成绩吗?
如图所示,一男生推铅球,铅球在点A处出手,出手时铅球离地面$\frac{5}{3}$m.铅球落地点在B处,铅球运行中在该男生前4m处(即0D=4)达到最高点,此时铅球离地面3m.根据图示的直角坐标系,你能算出该男生推铅球的成绩吗?