题目内容
8.解方程组:$\left\{\begin{array}{l}{{x}^{2}-6xy+9{y}^{2}=9}\\{{x}^{2}-{y}^{2}-4x+4y=0}\end{array}\right.$.分析 先将原方程组变形为$\left\{\begin{array}{l}{(x-3y+3)(x-3y-3)=0}\\{(x+y-4)(x-y)=0}\end{array}\right.$,再变形为$\left\{\begin{array}{l}{x-3y+3=0}\\{x+y-4=0}\end{array}\right.,\left\{\begin{array}{l}{x-3y+3=0}\\{x-y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-3y-3=0}\\{x+y-4=0}\end{array}\right.,\left\{\begin{array}{l}{x-3y-3=0}\\{x-y=0}\end{array}\right.$,最后解这四个二元一次方程组求出其解即可.
解答 解:原方程组变形为:
$\left\{\begin{array}{l}{(x-3y+3)(x-3y-3)=0}\\{(x+y-4)(x-y)=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x-3y+3=0}\\{x+y-4=0}\end{array}\right.,\left\{\begin{array}{l}{x-3y+3=0}\\{x-y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-3y-3=0}\\{x+y-4=0}\end{array}\right.,\left\{\begin{array}{l}{x-3y-3=0}\\{x-y=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{9}{4}}\\{{y}_{1}=\frac{7}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3}{2}}\\{{y}_{2}=\frac{3}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{3}=\frac{15}{4}}\\{{y}_{3}=\frac{1}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{4}=-\frac{3}{2}}\\{{y}_{4}=-\frac{3}{2}}\end{array}\right.$.
点评 本题考查了二元一次方程组的解法的运用,解二元二次方程组的消元、降次思想的运用,因式分解的运用.解答时先将二元高次方程变形为二元一次方程组是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 买1根油条和1个大饼共2.5元 | B. | 2根油条比1个大饼便宜 | ||
| C. | 买2根油条和4个大饼共9元 | D. | 买5根油条和7个大饼共19元 |
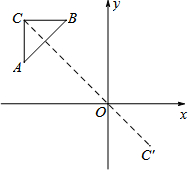 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,-3) | B. | (2,-1) | C. | (3,-2) | D. | (1,-2) |
 如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.
如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.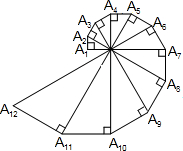 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.