题目内容
3.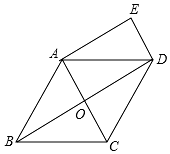 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;
(2)若AB=2$\sqrt{3}$,∠BCD=120°,连接CE,求CE的长.
分析 (1)首先根据菱形的性质,可得AC⊥BD,然后判断出四边形AODE是平行四边形,即可推得四边形AODE是矩形.
(2)在Rt△AEC中,求出AC、AE即可解决问题.
解答 (1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
又∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∴四边形AODE是矩形.
(2)解:∵∠BCD=120°,四边形ABCD是菱形,
∴∠BAD=∠BCD=120°,∠CAB=∠CAD=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=2$\sqrt{3}$,OB=OD=AE=3,
在Rt△AEC中,EC=$\sqrt{A{C}^{2}+A{E}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{3}^{2}}$=$\sqrt{21}$.
点评 此题主要考查了矩形的判定和性质的应用、以及菱形的性质和应用、等边三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题.

练习册系列答案
相关题目
2. 实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a<-b | B. | a<-3 | C. | a>-b | D. | a>-2 |
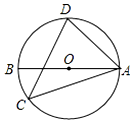 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD的度数为50°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40°,则∠BAD的度数为50°.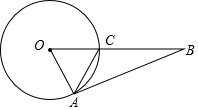 如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=$\frac{2}{3}$,则⊙O的半径长为$\frac{4\sqrt{13}}{3}$.
如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=$\frac{2}{3}$,则⊙O的半径长为$\frac{4\sqrt{13}}{3}$. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么AF的长是2$\sqrt{5}$;CH的长是$\sqrt{5}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么AF的长是2$\sqrt{5}$;CH的长是$\sqrt{5}$.