题目内容
2.解方程:(1)x2+2x=1;
(2)(x-3)2+2(x-3)=0;
(3)x2-9x+8=0;
(4)2x2+3x+1=0.
分析 (1)利用配方法解此方程即可;
(2)利用分解因式的方法解此方程即可;
(3)利用分解因式的方法解此方程即可;
(4)利用分解因式的方法解此方程即可.
解答 解:(1)∵x2+2x+1=1+1,
即(x+1)2=2,
∴x+1=$±\sqrt{2}$,
∴x1=-1$+\sqrt{2}$,x2=-1-$\sqrt{2}$;
(2)∵(x-3)2+2(x-3)=0,
∴(x-3)(x-3+2)=0,
∴x-3=0,或x-1=0,
∴x1=3,x2=1;
(3)∵x2-9x+8=0;
∴(x-1)(x-8)=0,
∴x-1=0,或x-8=0,
∴x1-1,x2=8;
(4)∵2x2+3x+1=0,
∴(2x+1)(x+1)=0,
∴2x+1=0,或x+1=0,
∴x1=-$\frac{1}{2}$,x2=-1.
点评 本题考查了解方程的方法-因式分解法和配方法,熟记解一元二次方程的方法是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.地球上陆地的面积约为148 000 000km2,这个数用科学记数法可以表示为( )
| A. | 148×106km2 | B. | 14.8×107km2 | C. | 1.48×108km2 | D. | 1.48×109km2 |
 如图,AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.(不写画法)
如图,AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.(不写画法) 如图,△ABD≌△CDB,若AB=4,AD=5,BD=6,∠ABD=30°,则CD=4.
如图,△ABD≌△CDB,若AB=4,AD=5,BD=6,∠ABD=30°,则CD=4.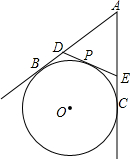 已知,如图,AB、AC是⊙O得切线,B、C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB、AC分别交于点D、E
已知,如图,AB、AC是⊙O得切线,B、C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB、AC分别交于点D、E 已知数轴:A点表示0,B点表示2,C点表示-1.5.
已知数轴:A点表示0,B点表示2,C点表示-1.5.