题目内容
7.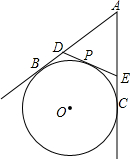 已知,如图,AB、AC是⊙O得切线,B、C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB、AC分别交于点D、E
已知,如图,AB、AC是⊙O得切线,B、C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB、AC分别交于点D、E(1)连接OD和OE,若∠A=50°,求∠DOE的度数.
(2)若AB=7,求△ADE的周长.
分析 (1)连接OB,OC,OD,OP,OE,根据切线的性质和切线长定理得到OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,于是求得∠OBA=∠OCA=90°,由于∠A=50°,求出∠BOC=360°-90°-90°-50°=130°,根据OB⊥AB,OP⊥DE,DB=DP,得到OD平分∠BOP,同理得OE平分∠POC,即可得到结论;
(2)根据切线长定理得到DB=DP,EP=EC,AB=AC,由等量代换即可得到结果.
解答  解:(1)连接OB,OC,OD,OP,OE,
解:(1)连接OB,OC,OD,OP,OE,
∵AB,AC,DE分别与⊙O相切,OB,OC,OP是⊙O的半径,
∴OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,
∴∠OBA=∠OCA=90°,
∵∠A=50°,
∴∠BOC=360°-90°-90°-50°=130°,
∵OB⊥AB,OP⊥DE,DB=DP,
∴OD平分∠BOP,
同理得:OE平分∠POC,
∴∠DOE=∠DOP+∠EOP=$\frac{1}{2}$(∠BOP+∠POC)=$\frac{1}{2}$∠BOC=65°,
(2)∵DB=DP,EP=EC,AB=AC,
∴△ADE的周长=AD+DE+AE
=AD+DP+EP+AE
=AD+BD+AE+EC
=AB+AC
=2AB=14.
点评 本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

练习册系列答案
相关题目
15. 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )| A. | △ABC≌△AFE | B. | △AFE≌△ADC | C. | △AFE≌△DFC | D. | △ABC≌△AED |
19. 图中几何体的左视图是( )
图中几何体的左视图是( )
 图中几何体的左视图是( )
图中几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 ,那么加上卡片上的数字;如果抽到的卡片形如
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
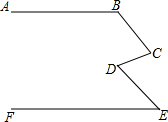 如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数.
如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数.