题目内容
10.已知等腰三角形的一边长为4,另一边长为8,则它的周长是( )| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
分析 题目给出等腰三角形有两条边长为8和4,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:当腰为8时,周长=8+8+4=20;
当腰长为4时,根据三角形三边关系可知此情况不成立;
根据三角形三边关系可知:等腰三角形的腰长只能为8,这个三角形的周长是20.
故选:D.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
20.函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≥-2 | C. | x≤-2 | D. | x>-2 |
1.某商品标价为a,若降价10%后出售,则实际售价为( )
| A. | 1.1a | B. | a | C. | 0.99a | D. | 0.9a |
18.把方程1-$\frac{x-3}{2}$=-$\frac{3x+5}{4}$去分母后,正确的是( )
| A. | 1-2x-3=3x+5 | B. | 1-2(x-3)=-3x+5 | C. | 4-2(x-3)=-3x+5 | D. | 4-2(x-3)=-(3x+5) |
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
| A. | 2cm | B. | 4cm | C. | 2cm或4cm | D. | 4cm或6cm |
15. 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,若CD=2,则OD=( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,若CD=2,则OD=( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,若CD=2,则OD=( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,若CD=2,则OD=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、4,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
20.下列式子由左到右的变形中,是因式分解且结果正确的为( )
| A. | x2-5x+6=x(x-5)+6 | B. | x2-5x+6=(x-2)(x-3) | C. | (x-2)(x-3)=x2-5x+6 | D. | x2-5x+6=(x+2)(x+3) |
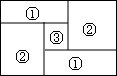 如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )
如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )