题目内容
13. 如图,已知∠EAC=90°,∠1+∠2=90°,∠1=∠3,DE∥BC.试说明:∠2=∠4.
如图,已知∠EAC=90°,∠1+∠2=90°,∠1=∠3,DE∥BC.试说明:∠2=∠4.
分析 先延长FA,CB交于点G,根据同角的余角相等,得出∠2=∠5,再根据等角的余角相等,得出∠5=∠G,进而得出∠2=∠G,最后根据平行线的性质,得到∠4=∠G,即可得到∠2=∠4.
解答  证明:如图,延长FA,CB交于点G,
证明:如图,延长FA,CB交于点G,
∵∠EAC=90°,
∴∠1+∠5=90°,
又∵∠1+∠2=90°,
∴∠2=∠5,
∵∠CAG=90°,
∴∠1+∠5=90°,∠3+∠G=90°,
又∵∠1=∠3,
∴∠5=∠G,
∴∠2=∠G,
∵DE∥BC,
∴∠4=∠G,
∴∠2=∠4.
点评 本题主要考查了平行线的性质以及余角的定义的运用,解决问题的关键是作辅助线构造三角形,运用同角(等角)的余角相等进行推导.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.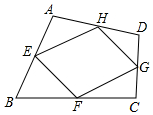 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
1.某商品标价为a,若降价10%后出售,则实际售价为( )
| A. | 1.1a | B. | a | C. | 0.99a | D. | 0.9a |
18.把方程1-$\frac{x-3}{2}$=-$\frac{3x+5}{4}$去分母后,正确的是( )
| A. | 1-2x-3=3x+5 | B. | 1-2(x-3)=-3x+5 | C. | 4-2(x-3)=-3x+5 | D. | 4-2(x-3)=-(3x+5) |
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
| A. | 2cm | B. | 4cm | C. | 2cm或4cm | D. | 4cm或6cm |
2.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、4,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
3.单项式-3x4y的( )
| A. | 系数为3,次数为4 | B. | 系数为-3,次数为4 | ||
| C. | 系数为3,次数为5 | D. | 系数为-3,次数为5 |
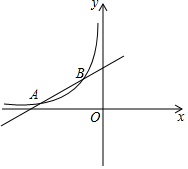 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?