题目内容
17.以半径为1的圆的内接正三角形、正方形、正六边形的边心距(圆心到边的距离)为三边作三角形,则该三角形的面积是( )| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
分析 由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
解答 解:如图1,
∵OC=1,
∴OD=1×sin30°=$\frac{1}{2}$;
如图2,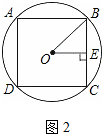
∵OB=1,
∴OE=1×sin45°=$\frac{\sqrt{2}}{2}$;
如图3,
∵OA=1,
∴OD=1×cos30°=$\frac{\sqrt{3}}{2}$,
则该三角形的三边分别为:$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$,
∵($\frac{1}{2}$)2+($\frac{\sqrt{2}}{2}$)2=($\frac{\sqrt{3}}{2}$)2,
∴该三角形是直角三角形,
∴该三角形的面积是$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{8}$,
故选:D.
点评 本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
7.下列四个数中,绝对值最大的是( )
| A. | 2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
| A. | 2cm | B. | 4cm | C. | 2cm或4cm | D. | 4cm或6cm |
12.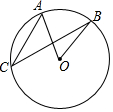 如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
 如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )
如图,⊙O中,弦AC与BC时两条弦,∠C=35°,则∠O的度数是( )| A. | 25° | B. | 35° | C. | 65° | D. | 70° |
2.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、4,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
9.要得到二次函数y=-x2+2x的图象,需将二次函数y=-x2的图象( )
| A. | 向左平移1个单位,再向上平移1个单位 | |
| B. | 向右平移1个单位,再向下平移1个单位 | |
| C. | 向左平移1个单位,再向下平移1个单位 | |
| D. | 向右平移1个单位,再向上平移1个单位 |
6.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )


| A. | 66° | B. | 60° | C. | 56° | D. | 54° |