题目内容
16．函数y=ax2-a与y=ax-a（a≠0）在同一坐标系中的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 可先根据一次函数的图象判断a的符号，再判断二次函数图象与实际是否相符，判断正误．
解答 解：A、由一次函数y=ax-a的图象可得：a＞0，此时二次函数y=ax2-a的图象应该开口向上，图象的两交点在坐标轴上，故A正确；
B、由一次函数y=ax-a的图象可得：a＜0，此时二次函数y=ax2-a的图象应该开口向下，图象的两交点不在坐标轴上，故B错误；
C、由一次函数y=ax-a的图象可得：a＞0，此时二次函数y=ax2-a的图象应该开口向上，图象的两交点不在坐标轴上，故C错误．
D、由一次函数y=ax-a的图象可得：a＜0，此时二次函数y=ax2-a的图象应该开口向下，图象的两交点不在坐标轴上，故D错误；
故选：A．
点评 应该熟记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．
练习册系列答案
相关题目
如图所示是一个带正六边形螺帽的螺杆示意图，请画出它的三视图．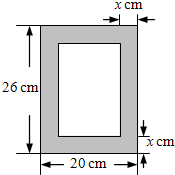
如图，某矩形相框长26cm，宽20cm，其四周相框边（图中阴影部分）的宽度相同，都是xcm，相框内部的面积（指图中较小矩形的面积）为ycm2，求y关于x的函数表达式，并写出自变量的取值范围．
1．直角三角形的一条直角边比斜边上的中线长2cm，且斜边为8cm，则两直角边的长分别为（ ）
| A． | 6，10 | B． | 6，2$\sqrt{7}$ | C． | 4，4$\sqrt{3}$ | D． | 2，2$\sqrt{15}$ |
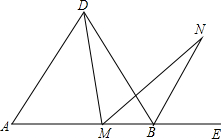已知点M是等边△ABD中边AB上任意一点（不与A、B重合），作∠DMN=60°，交∠DBA外角平分线于点N．