题目内容
1.直角三角形的一条直角边比斜边上的中线长2cm,且斜边为8cm,则两直角边的长分别为( )| A. | 6,10 | B. | 6,2$\sqrt{7}$ | C. | 4,4$\sqrt{3}$ | D. | 2,2$\sqrt{15}$ |
分析 由直角三角形斜边上的中线性质得出CD,再由已知条件得出AC,由勾股定理求出BC即可.
解答 解:如图所示:
∵CD是Rt△ABC斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=4cm,
∵直角三角形的一条直角边比斜边上的中线长2cm,
∴AC=2cm+4cm=6cm,
由勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$(cm);
故选:B.
点评 本题考查了勾股定理、直角三角形斜边上的中线性质;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
11.两实根和是3的一元二次方程为( )
| A. | x2+3x-4=0 | B. | x2-3x+4=0 | C. | x2-3x-4=0 | D. | x2+3x+4=0 |
12.如果2(x+3)的值与3(1-x)的值互为相反数,那么x等于( )
| A. | 9 | B. | 2 | C. | 3 | D. | 4 |
6.在同一直角坐标系中,P、Q分别是y=-x+3与y=3x-5的图象上的点,且P、Q关于x轴对称,则点P的坐标是( )
| A. | (-$\frac{1}{2}$,$\frac{7}{2}$) | B. | (-2,5) | C. | (1,2) | D. | (-4,7) |
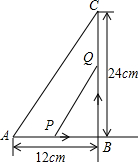 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2?
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2?



 图中有三个正方形,请你指出图中所有的全等三角形.
图中有三个正方形,请你指出图中所有的全等三角形.