题目内容
 如图,在平面直角坐标系中,四边形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
如图,在平面直角坐标系中,四边形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=| k |
| x |
(1)双曲线的另一支在第
(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若
| OD |
| OC |
| 1 |
| 2 |
考点:反比例函数综合题
专题:
分析:(1)由双曲线y=
的一支在第一象限,可得双曲线的另一支在第三象限,k的取值范围是:k>0;
(2)由点C的坐标为(2,2),AC∥OB,BC⊥OB,可得点A(
,2),E(2,
),即可得S阴影=S△ACE+S△OBE=
AC•CE+
k=
(2-
)2+
k=
(k-2)2+
,继而求得答案;
(3)首先延长CA交y轴于点M,过点D作DN⊥y轴于点N,易得△ODN∽△OCM,然后由相似三角形面积比等于相似比的平方,可得
=(
)2=(
)2=
,又由S△OAM=S△ODN=
,S△OAC=1,即可得:
=
,继而求得答案.
| k |
| x |
(2)由点C的坐标为(2,2),AC∥OB,BC⊥OB,可得点A(
| k |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 2 |
(3)首先延长CA交y轴于点M,过点D作DN⊥y轴于点N,易得△ODN∽△OCM,然后由相似三角形面积比等于相似比的平方,可得
| S△ODN |
| S△OCM |
| OD |
| OC |
| 1 |
| 2 |
| 1 |
| 4 |
| k |
| 2 |
| ||
1+
|
| 1 |
| 4 |
解答:解:(1)∵双曲线y=
的一支在第一象限,
∴双曲线的另一支在第三象限,k的取值范围是:k>0;
故答案为:三,k>0;
(2)∵点C的坐标为(2,2),AC∥OB,BC⊥OB,
∴点A(
,2),E(2,
),
∴AC=2-
,CE=2-
,
∴S阴影=S△ACE+S△OBE=
AC•CE+
k=
(2-
)2+
k=
(k-2)2+
,
∴当k=2时,阴影部分的面积S最小,
此时点E的坐标为:(2,1);
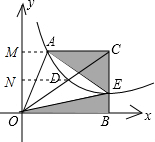 (3)延长CA交y轴于点M,过点D作DN⊥y轴于点N,
(3)延长CA交y轴于点M,过点D作DN⊥y轴于点N,
∴DN∥OB,BC⊥OB,
∵AC∥OB,CM⊥y轴,
∴△ODN∽△OCM,
∴
=(
)2=(
)2=
,
∵点A与点D在双曲线y=
的图象上,
∴S△OAM=S△ODN=
,
∵S△OAC=1,
∴
=
,
解得:k=
.
| k |
| x |
∴双曲线的另一支在第三象限,k的取值范围是:k>0;
故答案为:三,k>0;
(2)∵点C的坐标为(2,2),AC∥OB,BC⊥OB,
∴点A(
| k |
| 2 |
| k |
| 2 |
∴AC=2-
| k |
| 2 |
| k |
| 2 |
∴S阴影=S△ACE+S△OBE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 2 |
∴当k=2时,阴影部分的面积S最小,
此时点E的坐标为:(2,1);
 (3)延长CA交y轴于点M,过点D作DN⊥y轴于点N,
(3)延长CA交y轴于点M,过点D作DN⊥y轴于点N,∴DN∥OB,BC⊥OB,
∵AC∥OB,CM⊥y轴,
∴△ODN∽△OCM,
∴
| S△ODN |
| S△OCM |
| OD |
| OC |
| 1 |
| 2 |
| 1 |
| 4 |
∵点A与点D在双曲线y=
| k |
| x |
∴S△OAM=S△ODN=
| k |
| 2 |
∵S△OAC=1,
∴
| ||
1+
|
| 1 |
| 4 |
解得:k=
| 2 |
| 3 |
点评:此题属于反比例函数综合题,考查了待定系数求函数解析式的知识、相似三角形的判定与性质以及二次函数的最值问题.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的有( )
①对角线相等且互相垂直的四边形是菱形
②邻边相等的平行四边形是正方形
③对角线相等且互相平分的四边形是矩形
④顺次连接菱形各边中点所得的四边形是矩形
⑤有一个内角是60°的平行四边形是菱形.
①对角线相等且互相垂直的四边形是菱形
②邻边相等的平行四边形是正方形
③对角线相等且互相平分的四边形是矩形
④顺次连接菱形各边中点所得的四边形是矩形
⑤有一个内角是60°的平行四边形是菱形.
| A、1个 | B、2个 | C、3个 | D、4个 |
等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为( )
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为
,把△EFO缩小,则点E的对应点E′的坐标是( )
| 1 |
| 2 |
| A、(-2,1) |
| B、(-8,4) |
| C、(-2,1)或(2,-1) |
| D、(-8,4)或(8,-4) |
在下列图形中,属于中心对称图形的是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、平行四边形 |
在某文具店,一支铅笔的售价为1.2元,一支圆珠笔的售价为2元,该店在新年之际举行文具优惠销售活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.设该铅笔卖出x支,则可得的一元一次方程为( )
| A、0.8×1.2x+0.9×2(60-x)=87 |
| B、0.8×1.2x+0.9×2(60+x)=87 |
| C、0.9×2x+0.8×1.2(60+x)=87 |
| D、0.9×2x+0.8×1.2(60-x)=87 |
 如图,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=35°,求∠ABC的度数.
如图,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=35°,求∠ABC的度数.