Question

13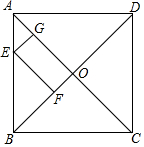．已知：如图，在正方形ABCD中，对角线AC、BD相交于AO，E是AB上的任意一点，EG⊥AC，EF⊥BD，垂足分别为G、F，求证：EG+EF=$\frac{1}{2}$AC．

Answer 1

分析 由S_△AOE+S_△BOE=S_△BOA即可解决问题．

解答 解：连接OE，
∵四边形ABCD是正方形，
∴AC⊥BD，BO=OA=$\frac{1}{2}$AC，
∵EG⊥AC，EF⊥BD，
∴S_△AOE+S_△BOE=S_△BOA，
∴$\frac{1}{2}$•AO•EG+$\frac{1}{2}$•OB•EF=$\frac{1}{2}$•OB•OA，
∴$\frac{1}{2}$×OB×EG+$\frac{1}{2}$×OB×EF=$\frac{1}{2}$•OB•OA，
∴EG+EF=OA，
∵OA=$\frac{1}{2}$AC，
∴EG+EF=$\frac{1}{2}$AC．

点评 本题考查正方形的性质，利用面积法是解决问题的关键，这里记住一个结论：等腰三角形底边上一点到两腰的距离之和等于腰上的高，填空题可以直接应用，属于中考常考题型．