题目内容
 把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.
把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.(1)如果AB=1,BC=
| 4 |
| 3 |
(2)如果AB=BC=1,使△NBC′≌△C′AE的C′还存在吗?若存在,请求出C′的位置;若不存在,请说明理由.
考点:翻折变换(折叠问题)
专题:
分析:(1)设BC′=x时,△NBC′≌△C′AE,先根据全等三角形的性质得出BN=AC′=1-x,于是NC=BC-BN=
+x,再由折叠的性质得到NC′=NC=
+x,然后在Rt△BNC′中利用勾股定理列出方程(
+x)2=x2+(1-x)2,解方程即可;
(2)设BC′=x时,△NBC′≌△C′AE,先根据全等三角形的性质得出BN=AC′=AB-BC′=1-x,验算NC=BC-BN=x,再由折叠的性质得到NC′=NC=x,然后在Rt△BNC′中根据斜边最长得出NC′>BC′,这与NC′=BC′=x矛盾,于是得出结论:如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)设BC′=x时,△NBC′≌△C′AE,先根据全等三角形的性质得出BN=AC′=AB-BC′=1-x,验算NC=BC-BN=x,再由折叠的性质得到NC′=NC=x,然后在Rt△BNC′中根据斜边最长得出NC′>BC′,这与NC′=BC′=x矛盾,于是得出结论:如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
解答:解:(1)设BC′=x时,△NBC′≌△C′AE,则BN=AC′=AB-BC′=1-x,NC=BC-BN=
-(1-x)=
+x.
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=
+x.
在Rt△BNC′中,∵∠B=90°,
∴NC′2=BC′2+BN2,
∴(
+x)2=x2+(1-x)2,
解得x=
,
∵
>2>AB,
∴x=
不合题意舍去,
∴x=
,
即当点C′在AB上距离点B
个单位时,可使△NBC′≌△C′AE;
(2)如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.理由如下:
设BC′=x时,△NBC′≌△C′AE,则BN=AC′=AB-BC′=1-x,NC=BC-BN=1-(1-x)=x.
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=x.
在Rt△BNC′中,∵∠B=90°,
∴NC′>BC′,
而NC′=BC′=x,
∴如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
| 4 |
| 3 |
| 1 |
| 3 |
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=
| 1 |
| 3 |
在Rt△BNC′中,∵∠B=90°,
∴NC′2=BC′2+BN2,
∴(
| 1 |
| 3 |
解得x=
4±2
| ||
| 3 |
∵
4+2
| ||
| 3 |
∴x=
4+2
| ||
| 3 |
∴x=
4-2
| ||
| 3 |
即当点C′在AB上距离点B
4-2
| ||
| 3 |
(2)如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.理由如下:
设BC′=x时,△NBC′≌△C′AE,则BN=AC′=AB-BC′=1-x,NC=BC-BN=1-(1-x)=x.
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=x.
在Rt△BNC′中,∵∠B=90°,
∴NC′>BC′,
而NC′=BC′=x,
∴如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.同时考查了直角三角形的性质及一元二次方程的解法.

练习册系列答案
相关题目
 如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y= 观察思考:
观察思考: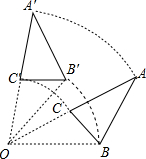 如图,将三角形ABC绕点O旋转得到三角形A′B′C′,且∠AOB=30°,∠AOB′=20°,则:
如图,将三角形ABC绕点O旋转得到三角形A′B′C′,且∠AOB=30°,∠AOB′=20°,则: 如图,河岸边CD的同侧有A,B两个村庄,现在河岸边CD修一个水电站P,是铺设连接A,B两村的管道最短,水站P应建在何处?
如图,河岸边CD的同侧有A,B两个村庄,现在河岸边CD修一个水电站P,是铺设连接A,B两村的管道最短,水站P应建在何处?