题目内容
 如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:作BD⊥OC于D,NE⊥x轴于E,如图,先利用坐标轴上点的坐标特征确定A(0,-4),B(2,0),设C点坐标为(m,2m-4),利用三角形面积公式得
×4×m=8,解得m=4,则C点坐标为(4,4),根据C点坐标可确定反比例函数解析式为y=
,且∠BOC=45°,OC=4
;设BE=t,则OE=t+2,利用反比例函数图形上点的坐标特征得N点坐标表示为(t+2,
),即NE=
,然后在Rt△OBD中根据等腰直角三角形的性质计算出OD=BD=
OB=
,则CD=3
;接着根据旋转的性质得∠MBN=135°,BN=BM,则∠CBN=45°,根据三角形外角性质易得∠1=∠2,于是可证明Rt△BEN∽Rt△CDB,利用相似比计算出t=6,则BE=6,NE=2,最后在Rt△BEN中,根据勾股定理可计算出BN=2
,即有BM=2
.
| 1 |
| 2 |
| 16 |
| x |
| 2 |
| 16 |
| t+2 |
| 16 |
| t+2 |
| ||
| 2 |
| 2 |
| 2 |
| 10 |
| 10 |
解答: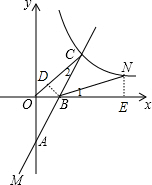 解:作BD⊥OC于D,NE⊥x轴于E,如图,
解:作BD⊥OC于D,NE⊥x轴于E,如图,
把x=0代入y=2x-4得y=4,
则A点坐标为(0,-4);
把y=0代入y=2x-4得2x-4=0,解得x=2,
则B点坐标为(2,0),
设C点坐标为(m,2m-4),
∵S△AOC=8,
∴
×4×m=8,解得m=4,
∴C点坐标为(4,4),
∴k=4×4=16,即反比例函数解析式为y=
,∠BOC=45°,OC=4
,
设BE=t,则OE=t+2,则N点坐标表示为(t+2,
),即NE=
,
在Rt△OBD中,∵OB=2,∠BOD=45°,
∴OD=BD=
OB=
,
∴CD=OC-OD=3
,
∵线段BM绕B点逆时针旋转135°,M落在双曲线上的点N处,
∴∠MBN=135°,BN=BM,
∴∠CBN=45°,
∵∠CBN+∠1=∠BOC+∠2,
∴∠1=∠2,
∴Rt△BEN∽Rt△CDB,
∴
=
,即
=
,
整理得t2+2t-48=0,
解得t1=-8(舍去),t2=6,
∴BE=6,NE=
=2,
在Rt△BEN中,BN=
=2
,
∴BM=2
.
 解:作BD⊥OC于D,NE⊥x轴于E,如图,
解:作BD⊥OC于D,NE⊥x轴于E,如图,把x=0代入y=2x-4得y=4,
则A点坐标为(0,-4);
把y=0代入y=2x-4得2x-4=0,解得x=2,
则B点坐标为(2,0),
设C点坐标为(m,2m-4),
∵S△AOC=8,
∴
| 1 |
| 2 |
∴C点坐标为(4,4),
∴k=4×4=16,即反比例函数解析式为y=
| 16 |
| x |
| 2 |
设BE=t,则OE=t+2,则N点坐标表示为(t+2,
| 16 |
| t+2 |
| 16 |
| t+2 |
在Rt△OBD中,∵OB=2,∠BOD=45°,
∴OD=BD=
| ||
| 2 |
| 2 |
∴CD=OC-OD=3
| 2 |
∵线段BM绕B点逆时针旋转135°,M落在双曲线上的点N处,
∴∠MBN=135°,BN=BM,
∴∠CBN=45°,
∵∠CBN+∠1=∠BOC+∠2,
∴∠1=∠2,
∴Rt△BEN∽Rt△CDB,
∴
| NE |
| BD |
| BE |
| CD |
| ||
|
| t | ||
3
|
整理得t2+2t-48=0,
解得t1=-8(舍去),t2=6,
∴BE=6,NE=
| 16 |
| 2+6 |
在Rt△BEN中,BN=
| BE2+NE2 |
| 10 |
∴BM=2
| 10 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了旋转的性质、等腰直角三角形的性质和相似三角形的判定与性质.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.
把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.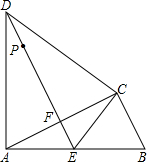 如图,△ABC中,∠ACB=90°,以AC为一边在△ABC作等边三角形ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE.
如图,△ABC中,∠ACB=90°,以AC为一边在△ABC作等边三角形ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE. 在△ABC中,点O为边AB,AC的垂直平分线的交点,请写出∠BOC和∠A的数量关系.
在△ABC中,点O为边AB,AC的垂直平分线的交点,请写出∠BOC和∠A的数量关系.