题目内容
有一个角是30°的直角木板,最短的边长为1,现将木板顺时针沿水平线翻滚,那么点A从开始至结束所走过的路程长度为多少?
考点:旋转的性质,弧长的计算
专题:计算题
分析:分类讨论:如图1,当∠A=30°时,BC=1,则AB=2BC=2,∠ABC=60°,由于Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,则∠ABA′=120°,然后根据弧长公式计算AA′的弧长;,如图2,当∠A=60°时,AC=1,则AB=2AC=2,∠ABC=30°,由于Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,则∠ABA′=150°,于是可根据弧长公式计算AA′的弧长.
解答:解:当∠A=30°时,BC=1,则AB=2BC=2,∠ABC=60°,则∠ABA′=120°,
将Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,如图1:
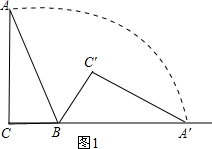
所以AA′的弧长=
=
π;
当∠A=60°时,AC=1,则AB=2AC=2,∠ABC=30°,则∠ABA′=150°,
将Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,如图2:
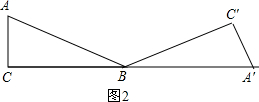
所以AA′的弧长=
=
π,
所以点A从开始至结束所走过的路程长度为
π或
π.
将Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,如图1:

所以AA′的弧长=
| 120•π•2 |
| 180 |
| 4 |
| 3 |
当∠A=60°时,AC=1,则AB=2AC=2,∠ABC=30°,则∠ABA′=150°,
将Rt△ABC顺时针沿水平线翻滚得到Rt△A′BC′,如图2:

所以AA′的弧长=
| 150•π•2 |
| 180 |
| 5 |
| 3 |
所以点A从开始至结束所走过的路程长度为
| 4 |
| 3 |
| 5 |
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了弧长公式.

练习册系列答案
相关题目
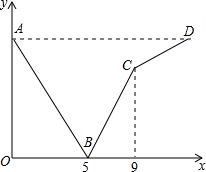 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶,设行驶时间为t(h),两车之间的距离为s(km) 图中折线A-B-C-D表示s与t之间的函数关系.试通过计算说明,当快车到达乙地时,慢车还要多少时间才能到达甲地?
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶,设行驶时间为t(h),两车之间的距离为s(km) 图中折线A-B-C-D表示s与t之间的函数关系.试通过计算说明,当快车到达乙地时,慢车还要多少时间才能到达甲地? 把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.
把矩形ABCD折叠,使点C落在AB上的C′处(不与A、B重合),点D落在D′处,此时,C′D′交AD于E,折痕为MN.