题目内容
17.若直线y=-2x-1与直线y=3x+m相交于第三象限内一点,则m的取值范围是( )| A. | -1<m<0 | B. | m<$\frac{3}{2}$ | C. | -1<m<$\frac{3}{2}$ | D. | 任意实数 |
分析 联立两直线解析式求出交点坐标,再根据交点在第三象限列出不等式组求解即可.
解答 解:联立 $\left\{\begin{array}{l}{y=-2x-1}\\{y=3x+m}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=-\frac{m+1}{5}}\\{y=\frac{2m-3}{5}}\end{array}\right.$,
∴交点坐标为(-$\frac{m+1}{5}$,$\frac{2m-3}{5}$),
∵两直线相交于第三象限,
∴$\left\{\begin{array}{l}{-\frac{m+1}{5}<0①}\\{\frac{2m-3}{5}<0②}\end{array}\right.$,
解不等式①得,m>-1,
解不等式②得,m<$\frac{3}{2}$,
所以,不等式组的解集是-1<m<$\frac{3}{2}$,
即实数m的取值范围是-1<m<$\frac{3}{2}$.
故选C.
点评 本题考查了两直线相交的问题,点的坐标与解不等式组,求出用m表示的交点坐标并列出不等式组是解题的关键,也是本题的难点.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.全国首届青运会在福州举行,下列体育图标中,可以看是中心对称图形的是( )
| A. |  皮筏艇 | B. |  花样游泳 | C. |  自行车 | D. |  柔道 |
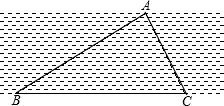 如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=31°,∠ACB=59°,BC=400m,求A到岸边BC的距离是多少米?(结果精确到1米).
如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=31°,∠ACB=59°,BC=400m,求A到岸边BC的距离是多少米?(结果精确到1米).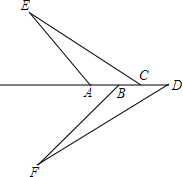 如图A、B、C、D、四点在同一直线上,请你从下面四项中选出三个选项作为条件,余下一个作为结论,构成一个真命题,并进行证明.
如图A、B、C、D、四点在同一直线上,请你从下面四项中选出三个选项作为条件,余下一个作为结论,构成一个真命题,并进行证明.