题目内容
11.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a,b,c.(1)已知a=40,c=41,求b;
(2)已知a=5,b=12,求c.
分析 (1)由勾股定理求出直角边b即可;
(2)由勾股定理求出斜边c即可.
解答 解:(1)∵∠C=90°,
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{4{1}^{2}-4{0}^{2}}$=9;
(2)∵∠C=90°,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
点评 本题考查了勾股定理;熟练掌握勾股定理是解决问题的关键,注意c是斜边.

练习册系列答案
相关题目
3.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,EF与AB、CD分别相交于M、N,EF⊥CD,∠1=63°,∠2=27°,试说明AB∥CD.
如图,EF与AB、CD分别相交于M、N,EF⊥CD,∠1=63°,∠2=27°,试说明AB∥CD. 如图所示,象棋盘上,若“将”位于点 (3,-2),“车”位于点(-1,-2),则“马”位于(6,1).
如图所示,象棋盘上,若“将”位于点 (3,-2),“车”位于点(-1,-2),则“马”位于(6,1).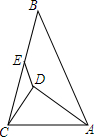 如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.
如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.