题目内容
观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，则2+6+10+14+…+2014的
值是 。
。
【考点】探索规律题（
数字的变化类）。
【分析】根据已知数字变化规律，得出
连续奇数之和为数字个数的平方
，进而
得出答案：
∵1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，
∴
∴左边括号中最后一个数字是2n－1。
∵2014=
，
∴由2n－1=1007解得n=504。
∴1+3+5+…+2014=10072=
。
练习册系列答案
相关题目
于点N，GH与BC的延长线交于点M，EH与DC交于点P，FG与DC的延长线交于点Q．设S表示矩形PCMH的面积，
表
示矩形NFQC的面积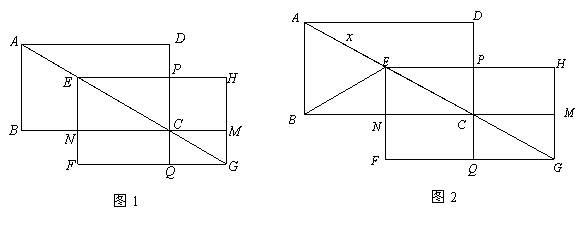
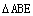
是
等腰三角形． 
为
边BC上的一点，AE⊥DE，AB=12，BE=
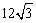，F为线段BE上一点，EF=7，连接AF。如图1，现有一张硬纸片△GMN，∠NGM=900，NG=6，MG=
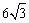，斜边MN与边BC在同一直线上，点N与点E重合，点G在线段DE上。如图2，△GMN从图1的位置出发，以每秒1个单位的速度沿EB向点B匀速移动，同时，点P从A点
出发，以每秒2个单位的速度沿AD向点D匀速移动，点Q为直线GN与线段AE的交点，连接PQ。当点G到达线段AE上时，△GMN和点P同时停止运动。设运动时间为t秒，解答问题：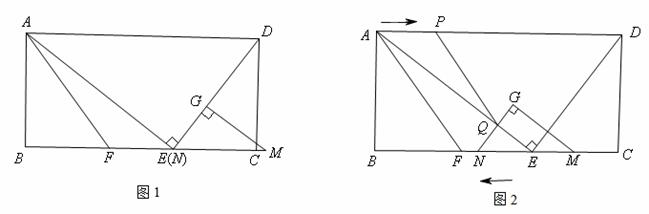
时，试用代数和几何两种方法探究
和
的大小关系。
，
。
。
B．
C．
D．
