题目内容
18.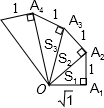 观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).
观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).
分析 这是一个规律性题目,第一个三角形的斜边正好是第二个三角形的直角边,依次进行下去,且有一个直角边的边长为1.从而可求出面积.
解答 解:根据勾股定理:
第一个三角形中:OA12=1+1,S1=1×1÷2;
第二个三角形中:OA22=OA12+1=1+1+1,S2=OA1×1÷2=$\sqrt{2}$×1÷2;
第三个三角形中:OA32=OA22+1=1+1+1+1,S3=OA2×1÷2=$\sqrt{3}$×1÷2;
…
第n个三角形中:Sn=$\sqrt{n}$×1÷2=$\frac{\sqrt{n}}{2}$.
故答案为:$\frac{\sqrt{n}}{2}$.
点评 本题主要考查了勾股定理的应用,根据勾股定理,逐一进行计算,从中寻求规律,进行解答是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
8.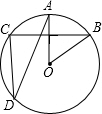 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
9.把一次函数y=-2x的图象向上平移3个单位长度,平移后,若y>0,则x的取值范围是( )
| A. | x>$\frac{3}{2}$ | B. | x<$\frac{3}{2}$ | C. | x>3 | D. | x<3 |
10.“校园安全”受到全社会的广泛关注,某校对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图(不完整).根据统计图中的信息,若全校有2050名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生人数为( )
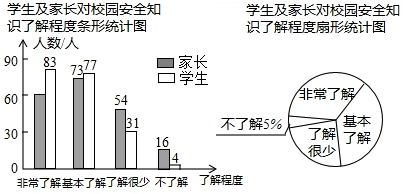

| A. | 1330 | B. | 1350 | C. | 1682 | D. | 1850 |
7.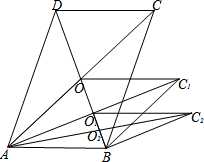 如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.
如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.
 如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.
如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.| A. | ${(\frac{1}{2})^{n-1}}$a | B. | ${(\frac{1}{2})^n}$a | C. | ${(\frac{1}{2})^{n+1}}$a | D. | ${(\frac{1}{3})^n}$a |
 如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.
如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.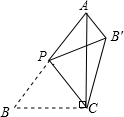 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1.
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是1. 已知S△ABC=12,AE是△ABC的中线,DE是△ABE的中线,求S△ADE.
已知S△ABC=12,AE是△ABC的中线,DE是△ABE的中线,求S△ADE.