题目内容
7.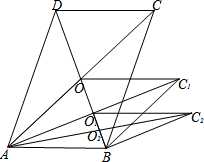 如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.
如图,平行四边形ABCD的面积为acm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1,以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn-1CnB的面积为( )cm2.| A. | ${(\frac{1}{2})^{n-1}}$a | B. | ${(\frac{1}{2})^n}$a | C. | ${(\frac{1}{2})^{n+1}}$a | D. | ${(\frac{1}{3})^n}$a |
分析 根据平行四边形的性质得出O1A=O1C1,O1B=O1O,求出S△AO1B=$\frac{1}{2}$S△ABC1=$\frac{1}{4}$S?ABC1D=$\frac{1}{8}$S?ABCD,求出平行四边形ABC1O的面积是AC1×BO1=$\frac{a}{2}$cm2,同理平行四边形ABC2O1的面积是$\frac{a}{4}$cm2,平行四边形ABC3O2的面积是$\frac{a}{8}$cm2,平行四边形ABC4O3的面积是$\frac{a}{16}$cm2,进而得到问题的规律,所以平行四边形AOn-1CnB的面积可求.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴O1A=O1C1,O1B=O1O,
∴S△AO1B=$\frac{1}{2}$S△ABC1=$\frac{1}{4}$S?ABC1D=$\frac{1}{8}$S?ABCD=$\frac{a}{8}$cm2,
∴平行四边形ABC1O的面积是:$\frac{a}{2}$cm2,
同理平行四边形ABC2O1的面积是$\frac{a}{4}$=($\frac{1}{2}$)2acm2,
平行四边形ABC3O2的面积是$\frac{a}{8}$=($\frac{1}{2}$)3acm2,
平行四边形ABC4O3的面积是$\frac{a}{16}$=($\frac{1}{2}$)4acm2,
平行四边形ABC5O4的面积是$\frac{a}{32}$=($\frac{1}{2}$)5cm2,
…以此类推AOn-1CnB的面积为:($\frac{1}{2}$)na.
故选:B.
点评 本题考查了平行四边形性质、三角形的面积等知识点,此题的关键是能根据求出的结果得出规律,注意:等底等高的三角形的面积相等.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
17.小明用100元钱去购买笔记本和钢笔共30件,如果每支钢笔5元,每个笔记本2元,那么小明最多能买( )支钢笔.
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
12.4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | ±$\sqrt{4}$ |
19.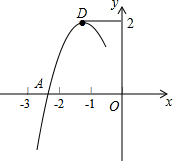 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
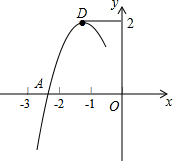 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
16.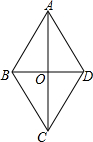 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )| A. | ∠ABC=60° | B. | ∠BC0=60° | C. | ∠ADO=60° | D. | ∠ADC=60° |
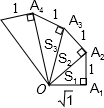 观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).
观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数). 如图,直线y=kx+b经过A(0,-3)和B(-3,0)两点.
如图,直线y=kx+b经过A(0,-3)和B(-3,0)两点.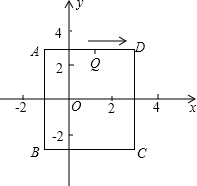 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$).
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$). 在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).
在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).