题目内容
8. 已知S△ABC=12,AE是△ABC的中线,DE是△ABE的中线,求S△ADE.
已知S△ABC=12,AE是△ABC的中线,DE是△ABE的中线,求S△ADE.
分析 先根据AD是△ABC的中线可知S△ADE=$\frac{1}{2}$S△ABC,再由DE是△ADC的中线可知S△ADE=$\frac{1}{2}$S△ADE,故可得出结论.
解答 解:∵AD是△ABC的中线,△ABC的面积为12,
∴S△ADE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6,
∵DE是△ABE的中线,
∴S△ADE=$\frac{1}{2}$S△ADE=$\frac{1}{2}$×6=3.
点评 本题考查的是三角形的面积,熟知三角形的中线将三角形的面积分为相等的两部分是解答此题的关键.

练习册系列答案
相关题目
19.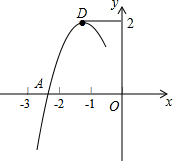 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
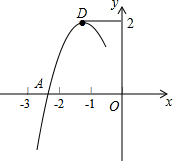 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②a+b+c<0;③a=c-2;④方程ax2+bx+c=0的根为-1.
其中正确的结论为( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
16.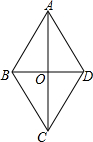 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
 如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )
如图,已知菱形ABCD,对角线AC、BD相交于O,∠BAD=60°,则( )| A. | ∠ABC=60° | B. | ∠BC0=60° | C. | ∠ADO=60° | D. | ∠ADC=60° |
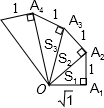 观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).
观察图形,分析、归纳,用含n的代数式表示第n个直角三角形的面积Sn=$\frac{\sqrt{n}}{2}$(n为正整数).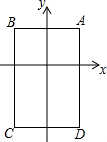 在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).
在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).