题目内容
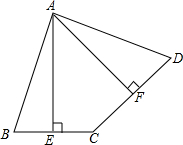 如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.
如图,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD.(1)求证:AB=AD;
(2)请问∠BAD,∠EAF之间有什么数量关系?并证明你的结论.
考点:全等三角形的判定与性质
专题:
分析:(1)连接AC,根据线段中点的定义可得BE=CE,然后利用“边角边”证明△ABE和△ACE全等,根据全等三角形对应边相等可得AB=AC,同理可得AD=AC,等量代换即可得证;
(2)根据全等三角形对应角相等可得∠BAE=∠CAE,同理可得∠DAF=∠CAF,然后求解即可.
(2)根据全等三角形对应角相等可得∠BAE=∠CAE,同理可得∠DAF=∠CAF,然后求解即可.
解答: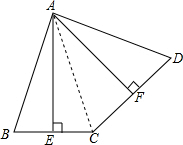 (1)证明:如图,连接AC,
(1)证明:如图,连接AC,
∵点E是BC的中点,
∴BE=CE,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在△ABE和△ACE中,
,
∴△ABE≌△ACE(SAS),
∴AB=AC,
同理可得AD=AC,
∴AB=AD;
(2)解:∠BAD=2∠EAF.
理由如下:∵△ABE≌△ACE,
∴∠BAE=∠CAE,
同理可得∠DAF=∠CAF,
∵∠BAD=∠BAE+∠CAE+∠CAF+∠DAF=2(∠CAE+∠CAF)=2∠EAF,
即∠BAD=2∠EAF.
 (1)证明:如图,连接AC,
(1)证明:如图,连接AC,∵点E是BC的中点,
∴BE=CE,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在△ABE和△ACE中,
|
∴△ABE≌△ACE(SAS),
∴AB=AC,
同理可得AD=AC,
∴AB=AD;
(2)解:∠BAD=2∠EAF.
理由如下:∵△ABE≌△ACE,
∴∠BAE=∠CAE,
同理可得∠DAF=∠CAF,
∵∠BAD=∠BAE+∠CAE+∠CAF+∠DAF=2(∠CAE+∠CAF)=2∠EAF,
即∠BAD=2∠EAF.
点评:本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目

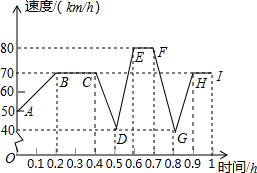 平川四中教生物的王老师驱车到屈吴山采集植物标本,在上山行驶过程中,要经过上坡、下坡、平路等路段,她的SUV在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,下面的图象表示了她开车在山区行驶过程中的速度随时间变化的情况.
平川四中教生物的王老师驱车到屈吴山采集植物标本,在上山行驶过程中,要经过上坡、下坡、平路等路段,她的SUV在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,下面的图象表示了她开车在山区行驶过程中的速度随时间变化的情况. 如图所示,∠B=∠C,AE是△ABC的外角∠DAC的平分线,试判断AE与BC的位置关系;并说明理由.
如图所示,∠B=∠C,AE是△ABC的外角∠DAC的平分线,试判断AE与BC的位置关系;并说明理由.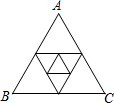 如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.
如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.