题目内容
15.如图,平面直角坐标系中,直线AB:y=-$\frac{1}{3}$x+b交y轴于点A(0,1),交x轴于点B,过点E(1,0)作x轴的垂线EF交AB于点D,点P从D出发,沿着射线ED的方向向上运动,设PD=n.(1)求直线AB的表达式;
(2)求△ABP的面积(用含n的代数式表示);
(3)若以P为直角顶点,PB为直角边在第一象限作等腰直角△BPC,请问随着点P的运动,点C是否也在同一直线上运动?若在同一直线上运动,请求出直线解析式;若不在同一直线上运动,请说明理由.

分析 (1)把A的坐标代入直线AB的解析式,即可求得b的值,然后在解析式中,令y=0,求得x的值,即可求得B的坐标;
(2)过点A作AM⊥PD,垂足为M,求得AM的长,即可求得△BPD和△PAB的面积,二者的和即可求得;
(3)利用等腰直角三角形的性质,判断出,△PCG≌△BPE,即可得出EG=n+$\frac{8}{3}$,CG=n+$\frac{2}{3}$,即可得出点C坐标,即可得出结论.
解答 解:(1)∵y=-$\frac{1}{3}$x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-$\frac{1}{3}$x+1.
当y=0时,0=-$\frac{1}{3}$x+1,解得x=3,
∴点B(3,0).
(2)如图,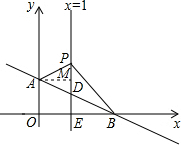 过点A作AM⊥PD,垂足为M,则有AM=1,
过点A作AM⊥PD,垂足为M,则有AM=1,
∵x=1时,y=-$\frac{1}{3}$x+1=$\frac{2}{3}$,P在点D的上方,
∴PD=n-$\frac{2}{3}$,
∴S△APD=$\frac{1}{2}$PD•AM=$\frac{1}{2}$×1×(n-$\frac{2}{3}$)=$\frac{1}{2}$n-$\frac{1}{3}$,
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴S△BPD=$\frac{1}{2}$PD×2=n-$\frac{2}{3}$,
∴S△PAB=S△APD+S△BPD=$\frac{1}{2}$n-$\frac{1}{3}$+n-$\frac{2}{3}$=$\frac{3}{2}$n-1
(3)随着点P的运动,点C是也在同一直线上运动,此直线的解析式为y=x+1,
如图1,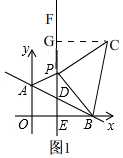 过点C作CG⊥EF,
过点C作CG⊥EF,
∴∠PCG+∠CPG=90°,
∵△BPC是等腰直角三角形,
∴BP=CP,∠BPC=90°,
∴∠CPG+∠BPE=90°.
∴∠PCG=∠BPE,
在△PCG和△BPE中,$\left\{\begin{array}{l}{∠PGC=∠BEP=90°}\\{∠PCG=∠BPE}\\{CP=BP}\end{array}\right.$,
∴△PCG≌△BPE,
∴CG=PE,PG=BE,
∵B(3,0),E(1,0),
∴BE=2,
∴PG=2,
∵点D在直线AB上,
∴D(1,$\frac{2}{3}$),
∴DE=$\frac{2}{3}$,
∵PD=n,
∴PE=DE+PD=n+$\frac{2}{3}$,EG=PE+PG=n+$\frac{2}{3}$+2=n+$\frac{8}{3}$,
∴CG=n+$\frac{2}{3}$,
∴C(n+$\frac{5}{3}$,n+$\frac{8}{3}$),
设C(x,y),
∴x=n+$\frac{5}{3}$,y=n+$\frac{8}{3}$,
∴y=x+1.
即:随着点P的运动,点C是也在同一直线上运动,此直线的解析式为y=x+1.
点评 此题是一次函数综合题,主要考查了坐标轴上点的特点,三角形的面积计算方法,等腰直角三角形的性质,全等三角形的判定和性质,解本题的关键是判断△PCG≌△BPE,坐标系中求三角形的面积的常用方法是作出三角形的铅锤高.

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )
如图,△ABC内接于⊙O,∠OAB=45°,则∠ACB的度数为( )| A. | 135° | B. | 130° | C. | 120° | D. | 140° |
| A. | 系数是-$\frac{1}{2}$,次数是4 | B. | 系数是-$\frac{1}{2}$,次数是3 | ||
| C. | 系数是-2,次数是4 | D. | 系数是-2,次数是3 |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
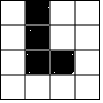 在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )
在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 甲、乙都可以 | B. | 甲 | C. | 乙 | D. | 无法确定 |
 如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )
如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )| A. | $\frac{3}{5}$S | B. | $\frac{4}{7}$S | C. | $\frac{5}{9}$S | D. | $\frac{6}{11}$S |